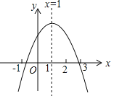题目内容
【题目】已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.
(1)如图1,若∠BAC=60°,点F与点C重合,
①求证:AF=AE+AD.
②求证:AD∥BC.
(2)如图2,若AD=AB,那么线段AF,AE,BC之间存在怎样的数量关系.

【答案】(1)①证明见解析;②证明见解析;(2)AF=AE+BC.
【解析】
(1)①由“SAS”可证△BCE≌△ACD,可得AD=BE,可得结论;
②由全等三角形的性质可得∠DAC=∠EBC=60°,由平行线的判定可得结论;
(2)如图2,在 FA 上截取 FM=AE,连接 DM,由“SAS”可证△AED≌△MFD,可得DA=DM=AB=AC,∠ADE=∠MDF,可证∠ADM=∠BAC,由“SAS”可证△ABC≌△DAM,可得AM=BC,可得结论.
证明:(1)①∵∠BAC=∠EDF=60°,AB=AC,DE=DF,
∴△ABC,△DEF 为等边三角形,
∴BC=AC,CE=CD,∠BCE+∠ACE=∠DCA+∠ECA=60°,
∴∠BCE=∠ACD,
在△BCE 和△ACD 中,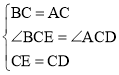 ,
,
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF,
即AF=AE+AD;
②∵△BCE≌△ACD,
∴∠DAC=∠EBC,
∵△ABC为等边三角形,
∴∠EBC=∠EAC=∠DAC=60°,
∴∠EBC+∠DAE=∠EBC+∠EAC+∠DAC=180°,
∴AD∥BC.
(2)如图2,在FA上截取FM=AE,连接DM,
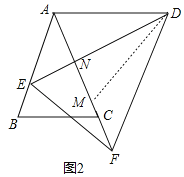
∵∠BAC=∠EDF,∠ANE=∠DNF,
∴∠AED=∠MFD,
在△AED 和△MFD中,
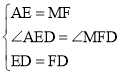 ,
,
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF,
∴∠ADM=∠BAC,
在△ABC 和△DAM 中,
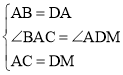
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.