题目内容
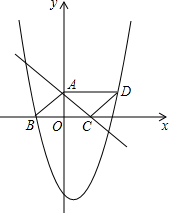 (2013•菏泽)如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-
(2013•菏泽)如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-| 3 |
| 4 |
| 1 |
| 8 |
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
分析:(1)根据一次函数解析式求出点A、点C坐标,再由△ABC是等腰三角形可求出点B坐标,根据平行四边形的性性质求出点D坐标,利用待定系数法可求出b、c的值,继而得出二次函数表达式.
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5-t,再由△APQ∽△CAO,利用对应边成比例可求出t的值,继而确定点P的位置;
②只需使△APQ的面积最大,就能满足四边形PDCQ的面积最小,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO,利用对应边成比例得出h的表达式,继而表示出△APQ的面积表达式,利用配方法求出最大值,即可得出四边形PDCQ的最小值,也可确定点P的位置.
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5-t,再由△APQ∽△CAO,利用对应边成比例可求出t的值,继而确定点P的位置;
②只需使△APQ的面积最大,就能满足四边形PDCQ的面积最小,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO,利用对应边成比例得出h的表达式,继而表示出△APQ的面积表达式,利用配方法求出最大值,即可得出四边形PDCQ的最小值,也可确定点P的位置.
解答:解:(1)由y=-
x+3,
令x=0,得y=3,所以点A(0,3);
令y=0,得x=4,所以点C(4,0),
∵△ABC是以BC为底边的等腰三角形,
∴B点坐标为(-4,0),
又∵四边形ABCD是平行四边形,
∴D点坐标为(8,3),
将点B(-4,0)、点D(8,3)代入二次函数y=
x2+bx+c,可得
,
解得:
,
故该二次函数解析式为:y=
x2-
x-3.
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5-t,
∵PQ⊥AC,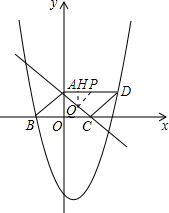
∴△APQ∽△CAO,
∴
=
,即
=
,
解得:t=
.
即当点P运动到距离A点
个单位长度处,有PQ⊥AC.
②∵S四边形PDCQ+S△APQ=S△ACD,且S△ACD=
×8×3=12,
∴当△APQ的面积最大时,四边形PDCQ的面积最小,
当动点P运动t秒时,AP=t,CQ=t,AQ=5-t,
设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO可得:
=
,
解得:h=
(5-t),
∴S△APQ=
t×
(5-t)=
(-t2+5t)=-
(t-
)2+
,
∴当t=
时,S△APQ达到最大值
,此时S四边形PDCQ=12-
=
,
故当点P运动到距离点A
个单位处时,四边形PDCQ面积最小,最小值为
.
| 3 |
| 4 |
令x=0,得y=3,所以点A(0,3);
令y=0,得x=4,所以点C(4,0),
∵△ABC是以BC为底边的等腰三角形,
∴B点坐标为(-4,0),
又∵四边形ABCD是平行四边形,
∴D点坐标为(8,3),
将点B(-4,0)、点D(8,3)代入二次函数y=
| 1 |
| 8 |
|
解得:
|
故该二次函数解析式为:y=
| 1 |
| 8 |
| 1 |
| 4 |
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5-t,
∵PQ⊥AC,

∴△APQ∽△CAO,
∴
| AP |
| AC |
| AQ |
| CO |
| t |
| 5 |
| 5-t |
| 4 |
解得:t=
| 25 |
| 9 |
即当点P运动到距离A点
| 25 |
| 9 |
②∵S四边形PDCQ+S△APQ=S△ACD,且S△ACD=
| 1 |
| 2 |
∴当△APQ的面积最大时,四边形PDCQ的面积最小,
当动点P运动t秒时,AP=t,CQ=t,AQ=5-t,
设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO可得:
| h |
| 3 |
| 5-t |
| 5 |
解得:h=
| 3 |
| 5 |
∴S△APQ=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 3 |
| 10 |
| 5 |
| 2 |
| 15 |
| 8 |
∴当t=
| 5 |
| 2 |
| 15 |
| 8 |
| 15 |
| 8 |
| 81 |
| 8 |
故当点P运动到距离点A
| 5 |
| 2 |
| 81 |
| 8 |
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、平行四边形的性质、相似三角形的判定与性质,解答本题的关键是找到满足题意时的相似三角形,利用对应边成比例的知识得出有关线段的长度或表达式,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
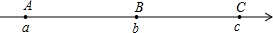 (2013•菏泽)如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
(2013•菏泽)如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
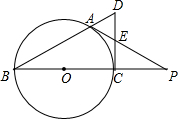 (2013•菏泽)如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(2013•菏泽)如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.