题目内容
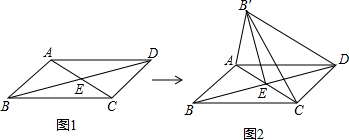
(2013•菏泽)如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为
.
| 2 |
| 2 |

分析:如图,连接BB′.根据折叠的性质知△BB′E是等腰直角三角形,则BB′=
BE.又B′E是BD的中垂线,则DB′=BB′.
| 2 |
解答: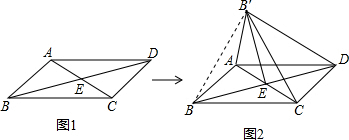 解:∵四边形ABCD是平行四边形,BD=2,
解:∵四边形ABCD是平行四边形,BD=2,
∴BE=
BD=1.
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,则BB′=
BE=
.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=
.
故答案是:
.
 解:∵四边形ABCD是平行四边形,BD=2,
解:∵四边形ABCD是平行四边形,BD=2,∴BE=
| 1 |
| 2 |
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,则BB′=
| 2 |
| 2 |
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=
| 2 |
故答案是:
| 2 |
点评:本题考查了平行四边形的性质,等腰三角形的判定与性质以及翻折变换(折叠的性质).推知DB′=BB′是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
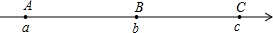 (2013•菏泽)如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
(2013•菏泽)如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )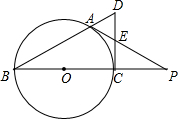 (2013•菏泽)如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(2013•菏泽)如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.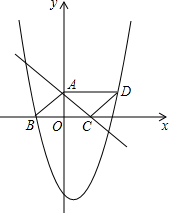 (2013•菏泽)如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-
(2013•菏泽)如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-