题目内容
【题目】下列边长相等的正多边形的组合中，不能镶嵌平面的是（ ）
A.正三角形和正方形B.正三角形和正六边形
C.正方形和正八边形D.正五边形和正方形
【答案】D
【解析】
首先分别求出各个正多边形每个内角的度数，再结合镶嵌的条件作出判断.
解：A项，正三角形的每个内角是60°，正方形的每个内角是90°，∵3×60°+2×90°=360°，∴能密铺；
B项，正三角形的每个内角是60°，正六边形的每个内角是120°，∵2×60°+2×120°=360°，∴能密铺；
C项，正八边形的每个内角是135°，正方形的每个内角是90°，∵2×135°+90°=360°，∴能密铺；
D项，正五边形的每个内角是108°，正方形的每个内角是90°，∵90m+108n=360，
，没有正整数解，∴此种情形不能密铺；
故选D.
练习册系列答案
阅读快车系列答案
相关题目
【题目】在学校组织的知识竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：
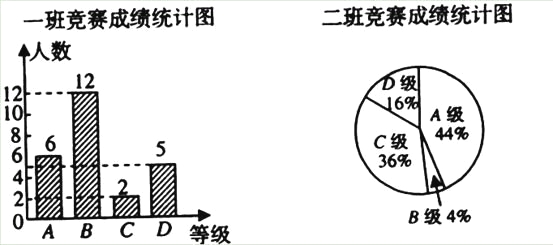
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班成绩在C级以上（包括C级）的人数为_______；
（2）请你将表格补充完整：
平均数（分） | 中位数（分） | 众数（分） | |
一班 | 87.6 | 90 | |
二班 | 87.6 | 100 |
（3）请从下列不同角度对这次竞赛成绩的结果进行
①从平均数和中位数的角度来比较一班和二班的成绩；
②从平均数和众数的角度来比较一班和二班的成绩；
③从B级以上（包括B级）的人数的角度来比较一班和二班的成绩．
