题目内容
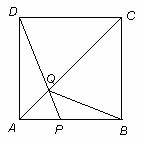
如图,在边长为4的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(1)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有△
上何处时,都有△![]() ≌△
≌△![]() ;
;
(2)当点![]() 在
在![]() 上运动到什么位置时,△
上运动到什么位置时,△![]() 的面积是正方形
的面积是正方形![]() 面积的
面积的![]() ;
;
(3)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,当点
,在整个运动过程中,当点![]() 运动到什么位置时,△
运动到什么位置时,△![]() 恰为等腰三角形.
恰为等腰三角形.
(1)证明:在正方形![]() 中,
中,
无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有
![]() =
=![]() ∠
∠![]() =∠
=∠![]()
![]() =
=![]()
 ∴△
∴△![]() ≌△
≌△![]()
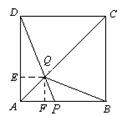
(2)解:△![]() 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的![]() 时,
时,
过点Q作![]()
![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,则
,则![]() =
= ![]()
![]()
![]() =
=![]() =
=![]()
∴![]() =
=![]()
由△![]() ∽△
∽△![]() 得
得 ![]() 解得
解得![]()
∴![]() 时,△
时,△![]() 的面积是正方形
的面积是正方形![]() 面积的
面积的![]()
(3)若△![]() 是等
是等![]() 腰三角形,则有
腰三角形,则有 ![]() =
=![]() 或
或![]() =
=![]() 或
或![]() =
=![]()
①当点![]() 运动到与点
运动到与点![]() 重合时,由四边形
重合时,由四边形![]() 是正方形知
是正方形知 ![]() =
=![]()
此时△![]() 是等腰三角形
是等腰三角形
②当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 与点
与点![]() 也重合,
也重合,
此时![]()
![]() =
=![]() , △
, △![]() 是等腰三角形
是等腰三角形
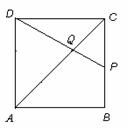
③解:如图,设点![]() 在
在![]() 边上运动到
边上运动到![]() 时,有
时,有![]() =
=![]()
 ∵
∵ ![]() ∥
∥![]() ∴∠
∴∠![]() =∠
=∠![]()
又∵∠![]() =∠
=∠![]() ∠
∠![]() =∠
=∠![]()
∴∠![]() =∠
=∠![]()
∴ ![]() =
=![]() =
=![]()
∵![]() =
=![]()
![]() =
= ![]() =4
=4
∴![]()
即当![]() 时,△
时,△![]() 是等腰
是等腰![]() 三角形
三角形

练习册系列答案
相关题目
 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,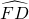 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.