题目内容
【题目】请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式![]() 解答下列问题:
解答下列问题:
已知:反比例函数![]() 与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数
与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数![]() 图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
【答案】见解析
【解析】
解由y=![]() 和y=x组成的方程组可得A、B两点的坐标分别为(
和y=x组成的方程组可得A、B两点的坐标分别为(![]() ,
,![]() )、(
)、(![]() ,
,![]() ),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y=
),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y=![]() 上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1-PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.
上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1-PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.
解:解由![]() 和y=x组成的方程组可得A、B两点的坐标分别为,(
和y=x组成的方程组可得A、B两点的坐标分别为,(![]() ,
,![]() )、(-
)、(-![]() ,-
,-![]() ),线段AB的长度=4
),线段AB的长度=4
∵点P(x0,y0)是反比例函数![]() 图象上一点,
图象上一点,
∴y0=![]()
∴PF1= =
=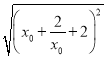 =|
=|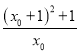 |,
|,
PF2= =
= =|
=| |,
|,
∴d=|PF1﹣PF2|=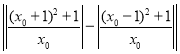 ,
,
当x0<0时,d=4;x0>0时,d=4.
∴无论点P的位置如何,线段AB的长度与d一定相等.
∴到两个定点的距离之差(取正值)是定值的点的集合(轨迹)是双曲线.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目