题目内容
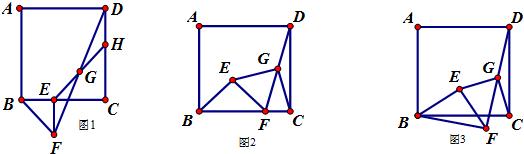
25、已知正方形ABCD和等腰直角三角形BEF,BE=EF,∠BEF=90°,按图1放置,使点E在BC上,取DF的中点G,连接EG,CG.
(1)延长EG交DC于H,试说明:DH=BE.
(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:EG=CG且EG⊥CG.在设法证明时他发现:若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?请写出来.
(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.
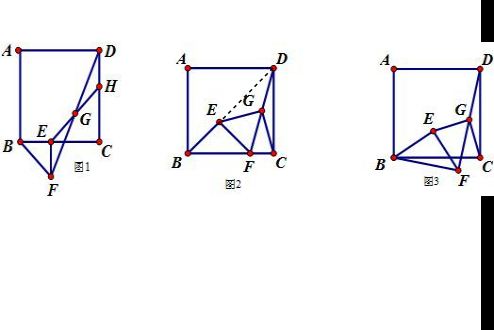
(1)延长EG交DC于H,试说明:DH=BE.
(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:EG=CG且EG⊥CG.在设法证明时他发现:若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?请写出来.
(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.

分析:(1)由∠BEF=90°,得到EF∥DH,而GF=GD,易证得△GEF≌△GHD,得EF=DH,而BE=EF,即可得到结论.
(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,得到D,E,B三点共线,而G为DF的中点,根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC,于是∠EGC=2∠EDC=90°,即得到结论.
(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,得到OG=BM,GM=OB,而EM=BM,OC=OB,得到EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF=90°,得∠EMG=∠GOC,则△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.
(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,得到D,E,B三点共线,而G为DF的中点,根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC,于是∠EGC=2∠EDC=90°,即得到结论.
(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,得到OG=BM,GM=OB,而EM=BM,OC=OB,得到EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF=90°,得∠EMG=∠GOC,则△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.
解答:(1)证明:∵∠BEF=90°,
∴EF∥DH,
∴∠EFG=∠GDH,
而∠EGF=∠DGH,GF=GD,
∴△GEF≌△GHD,
∴EF=DH,
而BE=EF,
∴DH=BE;
(2) 连接DB,如图2,
连接DB,如图2,
∵△BEF为等腰直角三角形,
∴∠EBF=45°,
而四边形ABCD为正方形,
∴∠DBC=45°,
∴D,E,B三点共线.
而∠BEF=90°,
∴△FED为直角三角形,
而G为DF的中点,
∴EG=GD=GC,
∴∠EGC=2∠EDC=90°,
∴EG=CG且EG⊥CG;
(3)第2问中的结论成立.理由如下:
连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,
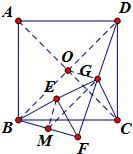
∵G为DF的中点,O为BD的中点,M为BF的中点,
∴OG∥BF,GM∥OB,
∴四边形OGMB为平行四边形,
∴OG=BM,GM=OB,
而EM=BM,OC=OB,
∴EM=OG,MG=OC,
∵∠DOG=∠GMF,
而∠DOC=∠EMF=90°,
∴∠EMG=∠GOC,
∴△MEG≌△OGC,
∴EG=CG,∠EGM=∠OCG,
又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,
∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,
∴EG=CG且EG⊥CG.
∴EF∥DH,
∴∠EFG=∠GDH,
而∠EGF=∠DGH,GF=GD,
∴△GEF≌△GHD,
∴EF=DH,
而BE=EF,
∴DH=BE;
(2)
 连接DB,如图2,
连接DB,如图2,∵△BEF为等腰直角三角形,
∴∠EBF=45°,
而四边形ABCD为正方形,
∴∠DBC=45°,
∴D,E,B三点共线.
而∠BEF=90°,
∴△FED为直角三角形,
而G为DF的中点,
∴EG=GD=GC,
∴∠EGC=2∠EDC=90°,
∴EG=CG且EG⊥CG;
(3)第2问中的结论成立.理由如下:
连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,

∵G为DF的中点,O为BD的中点,M为BF的中点,
∴OG∥BF,GM∥OB,
∴四边形OGMB为平行四边形,
∴OG=BM,GM=OB,
而EM=BM,OC=OB,
∴EM=OG,MG=OC,
∵∠DOG=∠GMF,
而∠DOC=∠EMF=90°,
∴∠EMG=∠GOC,
∴△MEG≌△OGC,
∴EG=CG,∠EGM=∠OCG,
又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,
∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,
∴EG=CG且EG⊥CG.
点评:本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了三角形全等的判定与性质、三角形中位线的性质、直角三角形斜边上的中线性质以及正方形的性质.

练习册系列答案
相关题目
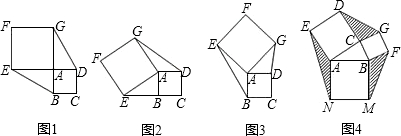
 24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.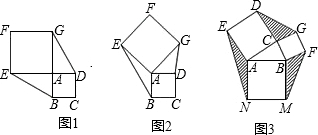
 如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.
如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.