题目内容
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.

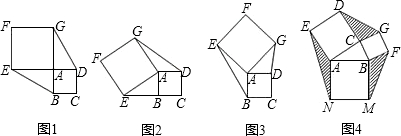
(1)如图,当点E旋转到DA的延长线上时,△ABE与△ADG面积之间的关系为:S△ABE
(2)如图,当正方形AEFG旋转任意一个角度时,S△ABE
(3)如图,四边形ABCD、四边形AEFG和四边形DGMN均为正方形,则S△ABE、S△ADG、S△CDN和S△GMF的关系是
(4)某小区中有一块空地,要在其中建三个正方形健身场所,其余空地(图中阴影部分)修成草坪,其中一个正方形的边长为6m.另外两个正方形的边长之和为10m,则草坪的最大面积为

(1)如图,当点E旋转到DA的延长线上时,△ABE与△ADG面积之间的关系为:S△ABE
=
=
S△ADG(填“<”“=”“>”);(2)如图,当正方形AEFG旋转任意一个角度时,S△ABE
=
=
S△ADG(填“<”“=”“>”),并说明理由;(3)如图,四边形ABCD、四边形AEFG和四边形DGMN均为正方形,则S△ABE、S△ADG、S△CDN和S△GMF的关系是
相等
相等
.(4)某小区中有一块空地,要在其中建三个正方形健身场所,其余空地(图中阴影部分)修成草坪,其中一个正方形的边长为6m.另外两个正方形的边长之和为10m,则草坪的最大面积为
48
48
m2.分析:(1)根据面积公式可直接看出△ABE与△ADG是等底等高的关系,所以面积相等;
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,过点G作△ADG中AD边上的高,交AD延长线于点Q.利用正方形和直角三角形的性质可证明△AEP≌△AGQ,即EP=QG,AB=AD,所以△ABE与△ADG也是等底等高,它们的面积关系是相等.
(3)与(2)的过程类似.
(4)设AD=6,AG=x,GD=10-x,利用海伦公式表示出一个三角形的面积,建立关于x的一元二次方程,求其最大值即可.
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,过点G作△ADG中AD边上的高,交AD延长线于点Q.利用正方形和直角三角形的性质可证明△AEP≌△AGQ,即EP=QG,AB=AD,所以△ABE与△ADG也是等底等高,它们的面积关系是相等.
(3)与(2)的过程类似.
(4)设AD=6,AG=x,GD=10-x,利用海伦公式表示出一个三角形的面积,建立关于x的一元二次方程,求其最大值即可.
解答:解:(1)相等,故答案为相等.
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,过点G作△ADG中AD边上的高,交AD延长线于点Q,如图,
∵正方形ABCD和正方形AEFG中,∠BAD=∠EAG=90°,
∴∠EAP+∠GAP=90°,
∠QAG+∠GAP=90°,
∴∠EAP=∠DAG,
∵AE=AG,∠EPA=∠AQG=90°,
∴Rt△AEP≌Rt△AGQ,
∴EP=QG,
而AB=AD,
∴S△ABE=
AB×EP=S△ADG=
AD×QD.
故答案为“=”.
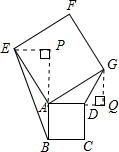
(3)根据(2)的推理过程可知,S△ABE=S△ADG=S△CDN=S△GMF.
故答案为“相等”.
(4)设AD=6,AG=x,GD=10-x,设△ADG的面积为S,
由海伦公式可知:S=
=4
,
当x=5时,S取得最小值,为12,
则由于四个三角形面积相等,故阴影部分的最大面积为12×4=48.
故答案为48.
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,过点G作△ADG中AD边上的高,交AD延长线于点Q,如图,
∵正方形ABCD和正方形AEFG中,∠BAD=∠EAG=90°,
∴∠EAP+∠GAP=90°,
∠QAG+∠GAP=90°,
∴∠EAP=∠DAG,
∵AE=AG,∠EPA=∠AQG=90°,
∴Rt△AEP≌Rt△AGQ,
∴EP=QG,
而AB=AD,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为“=”.

(3)根据(2)的推理过程可知,S△ABE=S△ADG=S△CDN=S△GMF.
故答案为“相等”.
(4)设AD=6,AG=x,GD=10-x,设△ADG的面积为S,
由海伦公式可知:S=
| {8(8-6)(8-x)[8-(10-x)]} |
| -(x-5)2+9 |
当x=5时,S取得最小值,为12,
则由于四个三角形面积相等,故阴影部分的最大面积为12×4=48.
故答案为48.
点评:本题考查了旋转的性质和相似三角形的性质,利用海伦公式求出一个阴影三角形的面积的最小值是解题的关键.

练习册系列答案
相关题目
 24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.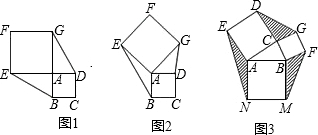
 如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.
如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.