题目内容
 24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.(1)如图1,连接DF、BF,证明:BF=DF;
(2)若将正方形AEFG绕点A按顺时针方向旋转,在旋转的过程中线段DF与BF的长还相等吗?若相等,请证明;若相不等,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
分析:(1)根据已知证明△DGF≌△BEF.
(2)观察DG的位置,找包含DG的三角形,要使两条线段相等,只要找到与之全等的三角形,即可找到与之相等的线段.
(2)观察DG的位置,找包含DG的三角形,要使两条线段相等,只要找到与之全等的三角形,即可找到与之相等的线段.
解答:(1)证明:∵四边形AEFG是正方形
∴GF=EF=AG=AE∠DGF=∠BEF=90°
∵四边形ABCD是正方形
∴AD=AB
∴AD-AG=AB-AE即 DG=BE
∴△DGF≌△BEF
∴BF=DF …5分
(2)BF≠DE 连接BE 有BE=DG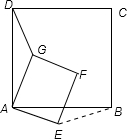
理由如下:∵∠DAB=∠GAE=90°
∴∠DAG=∠BAE
又AD=AB AG=AE
∴△DAG≌△BAE …9分
∴BE=DG …10分.
∴GF=EF=AG=AE∠DGF=∠BEF=90°
∵四边形ABCD是正方形
∴AD=AB
∴AD-AG=AB-AE即 DG=BE
∴△DGF≌△BEF
∴BF=DF …5分
(2)BF≠DE 连接BE 有BE=DG

理由如下:∵∠DAB=∠GAE=90°
∴∠DAG=∠BAE
又AD=AB AG=AE
∴△DAG≌△BAE …9分
∴BE=DG …10分.
点评:①本题考查了正方形的性质、全等三角形的性质以及全等三角形的判定,属于综合性的题目.
②本题是探求性试题,要求有比较高的逻辑思维.注意在平时的培养.
②本题是探求性试题,要求有比较高的逻辑思维.注意在平时的培养.

练习册系列答案
相关题目
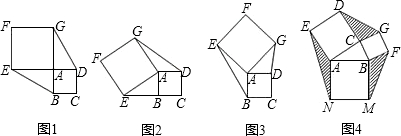
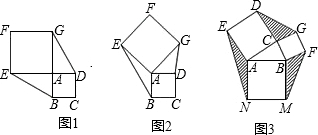
 如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.
如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.