题目内容
如图,已知AB和CD是⊙O的直径,CF∥DE,DE、CF分别交AB于点E、F.那么CF=DE吗?为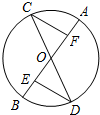 什么?
什么?解:∵CF∥DE,
∴∠C=∠D.
∵CD是⊙O的直径,
∴OC=
在△OCF和△ODE中,
|
∴△OCF≌△ODE,
∴CF=DE.
分析:要想证明CF=DE,只需利用ASA证明△OCF≌△ODE即可.
解答:解;∵CF∥DE,
∴∠C=∠D.(两直线平行,内错角相等) …(1分)
∵CD是⊙O的直径,
∴OC=
.(同圆的半径相等)…(1分)
在△OCF和△ODE中,
(已证)
(对顶角相等)
(已证)
…(2分)
∴△OCF≌△ODE,(ASA) …(1分)
∴CF=DE.(全等三角形的对应边相等) …(1分)
故答案为:两直线平行,内错角相等;OD,同圆的半径相等;∠C,∠D,∠DOE;ASA;全等三角形的对应边相等.
∴∠C=∠D.(两直线平行,内错角相等) …(1分)
∵CD是⊙O的直径,
∴OC=
| OD |
. |
在△OCF和△ODE中,
(已证)
(对顶角相等)
(已证)
|
∴△OCF≌△ODE,(ASA) …(1分)
∴CF=DE.(全等三角形的对应边相等) …(1分)
故答案为:两直线平行,内错角相等;OD,同圆的半径相等;∠C,∠D,∠DOE;ASA;全等三角形的对应边相等.
点评:本题考查了全等三角形的判定和性质,难度不大,注意掌握三角形全等的判定方法,并灵活运用.

练习册系列答案
相关题目
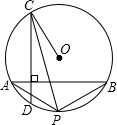 如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,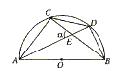
 如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,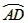 =
=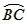 ,
,