题目内容
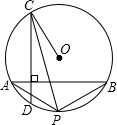如图，已知AB和CD是⊙O的两条弦，且AB⊥CD，连接OC，作∠OCD的平分线交⊙O于P，连接PA、PB，求证：PA=PB．
分析：如图，连接OP．利用等腰△AOP的底角相等、角平分的定义推知内错角∠3=∠1，所以CD∥OP．然后由平行线的性质证得OP⊥AB．最后根据垂径定理，圆周角、弧、弦间的关系证得结论．
解答：
证明：∵OC=OP，
∴∠1=∠2．
∵CP平分∠OCD，
∴∠2=∠3，
∴∠3=∠1，
∴CD∥OP，
∵CD⊥AB，
∴OP⊥AB．
∴
=
，
∴PA=PB．
证明：∵OC=OP，∴∠1=∠2．
∵CP平分∠OCD，
∴∠2=∠3，
∴∠3=∠1，
∴CD∥OP，
∵CD⊥AB，
∴OP⊥AB．
∴
 |
| AP |
|
| BP |
∴PA=PB．
点评：本题考查了垂径定理．证得OP⊥AB是解题的难点与关键点．
练习册系列答案
相关题目
什么？
如图，已知AB和CD是⊙O的两条弦，且AB⊥CD，连接OC，作∠OCD的平分线交⊙O于P，连接PA、PB，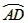
=
，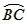