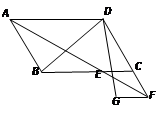题目内容
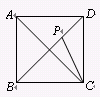
(1)如图1,在矩形ABCD中,AB=2BC,M是AB的中点.直接写出∠BMD与∠ADM的倍数关系;
(2)如图2,若四边形ABCD是平行四边形, AB=2BC,M是AB的中点,过C作CE⊥AD与AD所在直线交于点E.

①若∠A为锐角,则∠BME与∠AEM有怎样的倍数关系,并证明你的结论;
②当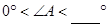 时,上述结论成立;
时,上述结论成立;
当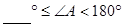 时,上述结论不成立.
时,上述结论不成立.
(2)如图2,若四边形ABCD是平行四边形, AB=2BC,M是AB的中点,过C作CE⊥AD与AD所在直线交于点E.

①若∠A为锐角,则∠BME与∠AEM有怎样的倍数关系,并证明你的结论;
②当
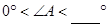 时,上述结论成立;
时,上述结论成立;当
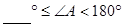 时,上述结论不成立.
时,上述结论不成立.(1)∠BMD= 3 ∠ADM
(2)联结CM,取CE的中点F,联结MF,交DC于N
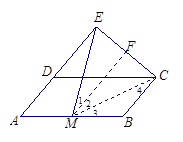
∵M是AB的中点,∴MF∥AE∥BC,
∴∠AEM=∠1,∠2=∠4,
∵AB=2BC,∴BM=BC,∴∠3=∠4.
∵CE⊥AE,∴MF⊥EC,又∵F是EC的中点,
∴ME=MC,∴∠1=∠2.
∴∠1=∠2=∠3.
∴∠BME =3∠AEM.
(3)当0°<∠A<120°时,结论成立;
当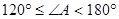 时,结论不成立.
时,结论不成立.
(2)联结CM,取CE的中点F,联结MF,交DC于N

∵M是AB的中点,∴MF∥AE∥BC,
∴∠AEM=∠1,∠2=∠4,
∵AB=2BC,∴BM=BC,∴∠3=∠4.
∵CE⊥AE,∴MF⊥EC,又∵F是EC的中点,
∴ME=MC,∴∠1=∠2.
∴∠1=∠2=∠3.
∴∠BME =3∠AEM.
(3)当0°<∠A<120°时,结论成立;
当
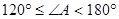 时,结论不成立.
时,结论不成立.(1)求出AM=AD,得到△ADM是等腰直角三角形,然后求出∠BMD与∠ADM的度数,从而得解;
(2)①连接CM,取CE的中点F,连接MF,交DC于N,根据平行线分线段成比例定理可得MF∥AE∥BC,再根据两直线平行,内错角相等可得∠AEM=∠1,∠2=∠4,再根据AB=2BC,M是AB的中点,利用等边对等角的性质求出∠3=∠4,根据三角形三线合一的性质求出∠1=∠2,从而得解;
②求出当点E与点A重合时的∠A的度数,即为临界值,小于临界值,点E在射线AD上,成立,否则不成立.
(2)①连接CM,取CE的中点F,连接MF,交DC于N,根据平行线分线段成比例定理可得MF∥AE∥BC,再根据两直线平行,内错角相等可得∠AEM=∠1,∠2=∠4,再根据AB=2BC,M是AB的中点,利用等边对等角的性质求出∠3=∠4,根据三角形三线合一的性质求出∠1=∠2,从而得解;
②求出当点E与点A重合时的∠A的度数,即为临界值,小于临界值,点E在射线AD上,成立,否则不成立.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 、
、 、
、 、
、 ,且
,且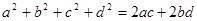 ,则这个四边形为 ;
,则这个四边形为 ; .
.