题目内容
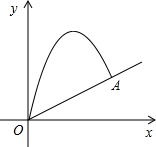
如图,点E(x1,y1)、F(x2,y2)在抛物线y=ax2+bx+c的对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.则S与y1、y2的数量关系式为:S=______.
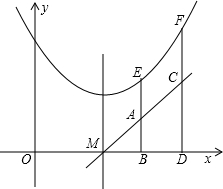

根据题意得:y1=ax12+bx1+c,y2=ax22+bx2+c,
点A的坐标为:(x1,2ax1+b),点C的坐标为:(x2,2ax2+b),
∴AB=2ax1+b,CD=2ax2+b,BD=x2-x1,
∵EB⊥BD,CD⊥BD,
∴AB∥CD,
∴四边形ABCD是直角梯形,
∴S=
(AB+CD)•BD=
(2ax1+b+2ax2+b)(x2-x1)=a(x2+x1)(x2-x1)+b(x2-x1)=(ax22+bx2)-(ax12+bx1)=(ax22+bx2+c)-(ax12+bx1+c)=y2-y1.
∴S与y1、y2的数量关系式为:S=y2-y1.
故答案为:y2-y1.
点A的坐标为:(x1,2ax1+b),点C的坐标为:(x2,2ax2+b),
∴AB=2ax1+b,CD=2ax2+b,BD=x2-x1,
∵EB⊥BD,CD⊥BD,
∴AB∥CD,
∴四边形ABCD是直角梯形,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S与y1、y2的数量关系式为:S=y2-y1.
故答案为:y2-y1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 一次函数
一次函数