题目内容
【题目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E. 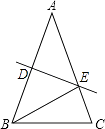
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
【答案】
(1)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=38°,
∵AB=AC,
∴∠ABC=∠C= ![]() =71°,
=71°,
∴∠EBC=∠ABC﹣∠ABE=71°﹣38°=33°
(2)解:当BC=13cm时,AB=AC=11.5cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=13cm+11.5cm=24.5cm;
当AB=AC=13cm时,则BC=10cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=10cm+13cm=23cm;
即△BCE的周长为24.5cm或23cm
【解析】(1)由DE是AB的垂直平分线,根据线段垂直平分线的性质得出AE=BE,则可求得∠ABE的度数,又由AB=AC,根据等边对等角与三角形内角和定理,即可求得∠ABC的度数,继而求得答案;(2)求出AC和BC的值,再根据线段垂直平分线的性质得出AE=BE,求出△BCE的周长=AC+BC,代入求出即可.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某校校园足球训练队队员的年龄有13、14、15、16四种年龄,统计结果如表:
年龄(岁) | 13 | 14 | 15 | 16 |
人数(个) | 14 | 15 | 16 | 17 |
根据表中信息可以判断该足球训练队队员年龄的众数为( )
A.14
B.15
C.16
D.17