Question

【题目】如图，⊙O是以Rt△ABC的直角边AC 为直径的圆，与斜边AB相交于点D，过D作DH⊥AC，垂足为H，又过D点作直线交BC于E，使∠HDE = 2∠A．求证：

(1) DE是⊙O的切线；(2) OE是Rt△ABC的中位线．

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】试题分析：(1)连接OD，通过三角形的外角证出∠HDE =∠HOD，再根据垂直定义利用等量代换证出∠HDE +∠ODH = 90，即可通过垂直证明结论.

(2)通过全等证出OE∥AB，再根据O是AC中点，即可得到结论.

证明：(1) 连结OD，则OD是⊙O的半径．

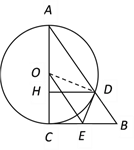
∵　∠HDE = 2∠A，∠DOH = 2∠A，∴　∠HDE =∠HOD．

∵　DH⊥AC，∴　∠DOH +∠ODH = 90，

∴　∠HDE +∠ODH = 90， 即OD⊥DE． ∴DE是⊙O的切线．

(2) ∵　DE是⊙O的切线，

∴　∠ODE = 90，又OC = OD，OE = OE，

∴　△ODE≌△OCE， ∴　∠COE =∠DOE．

又 ∵　∠COD = 2∠A， ∴　∠COE =∠A，

∴　OE∥AB，又AO = OC，

∴　OE是Rt△ABC的中位线．