题目内容
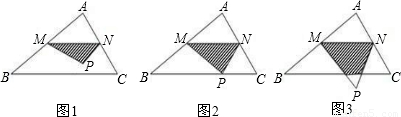
(2007•龙岩)如图1,在△ABC中,∠A=90°,AB=4,AC=3.M是边AB上的动点(M不与A,B重合),MN∥BC交AC于点N,△AMN关于MN的对称图形是△PMN.设AM=x.(1)用含x的式子表示△AMN的面积(不必写出过程);
(2)当x为何值时,点P恰好落在边BC上;
(3)在动点M的运动过程中,记△PMN与梯形MBCN重叠部分的面积为y,试求y关于x的函数关系式;并求x为何值时,重叠部分的面积最大,最大面积是多少?
【答案】分析:(1)因为MN∥BC,所以△AMN∽△ABC,所以根据相似三角形的性质即可求得MN的值与MN边上的高的值,即可求得面积;
(2)根据轴对称的性质,可求得相等的线段与角,可得点M是AB中点,即当x= AB=2时,点P恰好落在边BC上;
AB=2时,点P恰好落在边BC上;
(3)分两种情况讨论:①当0<x≤2时,易见y= x2.(8分)
x2.(8分)
②当2<x<4时,如图3,设PM,PN分别交BC于E,F
由(2)知ME=MB=4-x∴PE=PM-ME=x-(4-x)=2x-4
由题意知△PEF∽△ABC,利用相似三角形的性质即可求得.
解答:解:(1)S△AMN= x2(3);
x2(3);
(2)如图2,由轴对称性质知:AM=PM,∠AMN=∠PMN,(4分)
又MN∥BC,∴∠PMN=∠BPM,∠AMN=∠B,(5)
∴∠B=∠BPM∴AM=PM=BM(6分)
∴点M是AB中点,即当x= AB=2时,点P恰好落在边BC上.(7分)
AB=2时,点P恰好落在边BC上.(7分)
(3)(i)以下分两种情况讨论:
①当0<x≤2时,易见y= x2(8分)
x2(8分)
②当2<x<4时,如图3,设PM,PN分别交BC于E,F
由(2)知ME=MB=4-x,
∴PE=PM-ME=x-(4-x)=2x-4
由题意知△PEF∽△ABC,
∴ ,
,
∴
∴
∴y=
(ii)∵当0<x≤2时,y= x2
x2
∴易知y最大= (11分)
(11分)
又∵当2<x<4时,y= x2+6x-6=
x2+6x-6= (x-
(x- )2+2.
)2+2.
∴当 时(符合2<x<4),y最大=2,(12分)
时(符合2<x<4),y最大=2,(12分)
综上所述,当 时,重叠部分的面积最大,其值为2.(13分)
时,重叠部分的面积最大,其值为2.(13分)

点评:此题考查了折叠问题,要注意对应的线段对应的角相等,此题还考查了相似三角形的性质,解题的关键是数形结合思想的应用.
(2)根据轴对称的性质,可求得相等的线段与角,可得点M是AB中点,即当x=
 AB=2时,点P恰好落在边BC上;
AB=2时,点P恰好落在边BC上;(3)分两种情况讨论:①当0<x≤2时,易见y=
 x2.(8分)
x2.(8分)②当2<x<4时,如图3,设PM,PN分别交BC于E,F
由(2)知ME=MB=4-x∴PE=PM-ME=x-(4-x)=2x-4
由题意知△PEF∽△ABC,利用相似三角形的性质即可求得.
解答:解:(1)S△AMN=
 x2(3);
x2(3);(2)如图2,由轴对称性质知:AM=PM,∠AMN=∠PMN,(4分)
又MN∥BC,∴∠PMN=∠BPM,∠AMN=∠B,(5)
∴∠B=∠BPM∴AM=PM=BM(6分)
∴点M是AB中点,即当x=
 AB=2时,点P恰好落在边BC上.(7分)
AB=2时,点P恰好落在边BC上.(7分)(3)(i)以下分两种情况讨论:
①当0<x≤2时,易见y=
 x2(8分)
x2(8分)②当2<x<4时,如图3,设PM,PN分别交BC于E,F
由(2)知ME=MB=4-x,
∴PE=PM-ME=x-(4-x)=2x-4
由题意知△PEF∽△ABC,
∴
 ,
,∴

∴

∴y=

(ii)∵当0<x≤2时,y=
 x2
x2∴易知y最大=
 (11分)
(11分)又∵当2<x<4时,y=
 x2+6x-6=
x2+6x-6= (x-
(x- )2+2.
)2+2.∴当
 时(符合2<x<4),y最大=2,(12分)
时(符合2<x<4),y最大=2,(12分)综上所述,当
 时,重叠部分的面积最大,其值为2.(13分)
时,重叠部分的面积最大,其值为2.(13分)
点评:此题考查了折叠问题,要注意对应的线段对应的角相等,此题还考查了相似三角形的性质,解题的关键是数形结合思想的应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC. (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC. (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.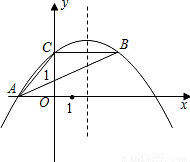 (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.