题目内容
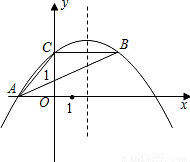 (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.(1)求抛物线的对称轴;
(2)写出A,B,C三点的坐标并求抛物线的解析式;
(3)探究:若点P是抛物线对称轴上且在x轴下方的动点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P坐标;不存在,请说明理由.
【答案】分析:(1)根据抛物线的解析式,利用对称轴公式,可直接求出其对称轴.
(2)令x=0,可求出C点坐标,由BC∥x轴可知B,C关于抛物线的对称轴对称,可求出B点坐标,根据AC=BC可求出A点坐标.
(3)分三种情况讨论:
①以AB为腰且顶角为∠A,先求出AB的值,再利用等腰三角形的性质结合勾股定理求出P1N的长,即可求出P1的坐标;
②以AB为腰且顶角为角B,根据MN的长和MP2的长,求出P2的纵坐标,已知其横坐标,可得其坐标;
③以AB为底,顶角为角P时,依据Rt△P3CK∽Rt△BAQ即可求出OK和P3K的长,可得P3坐标.
解答: 解:(1)抛物线的对称轴x=-
解:(1)抛物线的对称轴x=- =
= ;(2分)
;(2分)
(2)由抛物线y=ax2-5ax+4可知C(0,4),对称轴x=- =
= ,
,
∴BC=5,B(5,4),又AC=BC=5,OC=4,
在Rt△AOC中,由勾股定理,得AO=3,
∴A(-3,0)B(5,4)C(0,4)(5分)
把点A坐标代入y=ax2-5ax+4中,
解得a=- ,(6)
,(6)
∴y=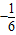 x2+
x2+ x+4.(7分)
x+4.(7分)
(3)存在符合条件的点P共有3个.以下分三类情形探索.
设抛物线对称轴与x轴交于N,与CB交于M.
过点B作BQ⊥x轴于Q,
易得BQ=4,AQ=8,AN=5.5,BM= .
.
①以AB为腰且顶角为角A的△PAB有1个:△P1AB.
∴AB2=AQ2+BQ2=82+42=80(8分)
在Rt△ANP1中,P1N= =
= =
= =
= ,
,
∴P1( ,-
,- ).(9分)
).(9分)
②以AB为腰且顶角为角B的△PAB有1个:△P2AB.
在Rt△BMP2中MP2= =
=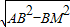
=
= ,(10分)
,(10分)
∴P2=( ,
, ).(11分)
).(11分)
③以AB为底,顶角为角P的△PAB有1个,即△P3AB.
画AB的垂直平分线交抛物线对称轴于P3,此时平分线必过等腰△ABC的顶点C.
过点P3作P3K垂直y轴,垂足为K,
∵∠CP3K=∠ABQ,∠CKP3=∠AQB,
∴Rt△P3CK∽Rt△BAQ.
∴ =
= =
= .
.
∵P3K=2.5
∴CK=5于是OK=1,(13分)
∴P3(2.5,-1).(14分)
点评:此题考查了用对称轴公式求函数对称轴方程,用待定系数法求函数解析式等基础知识,还结合等腰三角形的性质考查了点的存在性问题,有一定的开放性.
(2)令x=0,可求出C点坐标,由BC∥x轴可知B,C关于抛物线的对称轴对称,可求出B点坐标,根据AC=BC可求出A点坐标.
(3)分三种情况讨论:
①以AB为腰且顶角为∠A,先求出AB的值,再利用等腰三角形的性质结合勾股定理求出P1N的长,即可求出P1的坐标;
②以AB为腰且顶角为角B,根据MN的长和MP2的长,求出P2的纵坐标,已知其横坐标,可得其坐标;
③以AB为底,顶角为角P时,依据Rt△P3CK∽Rt△BAQ即可求出OK和P3K的长,可得P3坐标.
解答:
 解:(1)抛物线的对称轴x=-
解:(1)抛物线的对称轴x=- =
= ;(2分)
;(2分)(2)由抛物线y=ax2-5ax+4可知C(0,4),对称轴x=-
 =
= ,
,∴BC=5,B(5,4),又AC=BC=5,OC=4,
在Rt△AOC中,由勾股定理,得AO=3,
∴A(-3,0)B(5,4)C(0,4)(5分)
把点A坐标代入y=ax2-5ax+4中,
解得a=-
 ,(6)
,(6)∴y=
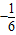 x2+
x2+ x+4.(7分)
x+4.(7分)(3)存在符合条件的点P共有3个.以下分三类情形探索.
设抛物线对称轴与x轴交于N,与CB交于M.
过点B作BQ⊥x轴于Q,
易得BQ=4,AQ=8,AN=5.5,BM=
 .
.①以AB为腰且顶角为角A的△PAB有1个:△P1AB.
∴AB2=AQ2+BQ2=82+42=80(8分)
在Rt△ANP1中,P1N=
 =
= =
= =
= ,
,∴P1(
 ,-
,- ).(9分)
).(9分)②以AB为腰且顶角为角B的△PAB有1个:△P2AB.
在Rt△BMP2中MP2=
 =
=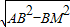
=

=
 ,(10分)
,(10分)∴P2=(
 ,
, ).(11分)
).(11分)③以AB为底,顶角为角P的△PAB有1个,即△P3AB.
画AB的垂直平分线交抛物线对称轴于P3,此时平分线必过等腰△ABC的顶点C.
过点P3作P3K垂直y轴,垂足为K,
∵∠CP3K=∠ABQ,∠CKP3=∠AQB,
∴Rt△P3CK∽Rt△BAQ.
∴
 =
= =
= .
.∵P3K=2.5
∴CK=5于是OK=1,(13分)
∴P3(2.5,-1).(14分)
点评:此题考查了用对称轴公式求函数对称轴方程,用待定系数法求函数解析式等基础知识,还结合等腰三角形的性质考查了点的存在性问题,有一定的开放性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC. (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC. (2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(2007•龙岩)如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.