题目内容
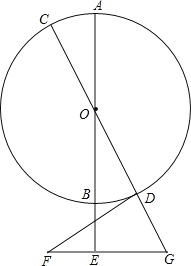
【题目】如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.
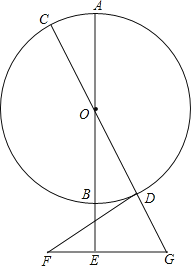
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
【答案】(1)⊙O半径是2.(2)见解析
【解析】
试题分析:(1)⊙0半径为R,则OD=OB=R,在Rt△OEG中,∠OEG=90°,由勾股定理得出方程(R+3)2=(R+2)2+32,求出即可;
(2)证△FDG≌△OEG,推出∠FDG=∠OEG=90°,求出OD⊥DF,根据切线的判定推出即可.
(1)解:设⊙0半径为R,则OD=OB=R,
在Rt△OEG中,∠OEG=90°,由勾股定理得:OG2=OE2+EG2,
∴(R+3)2=(R+2)2+32,
R=2,
即⊙O半径是2.
(2)证明:∵OB=OD=2,
∴OG=2+3=5,GF=2+3=5=OG,
∵在△FDG和△OEG中

∴△FDG≌△OEG(SAS),
∴∠FDG=∠OEG=90°,
∴∠ODF=90°,
∴OD⊥DF,
∵OD为半径,
∴DF是⊙O的切线.

练习册系列答案
相关题目