题目内容
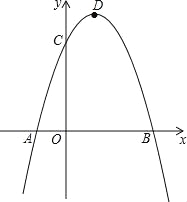
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)证明参见解析;(3)存在,P(![]() ,
,![]() )或P(2,3).
)或P(2,3).
【解析】
试题分析:(1)将A(﹣1,0)、C(0,3),代入二次函数y=ax2+bx﹣3a,求得a、b的值即可确定二次函数的解析式;(2)分别求得线段BC、CD、BD的长,利用勾股定理的逆定理进行判定即可;(3)分以CD为底和以CD为腰两种情况讨论.运用两点间距离公式建立起P点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解.
试题解析:(1)∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),∴将A(﹣1,0)、C(0,3),代入,得![]() ,解得
,解得![]() ,∴抛物线的解析式为y=﹣x2+2x+3;(2)如图,连接DC、BC、DB,由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),∴CD=
,∴抛物线的解析式为y=﹣x2+2x+3;(2)如图,连接DC、BC、DB,由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),∴CD=![]() =
=![]() ,BC=
,BC=![]() =3
=3![]() ,BD=
,BD=![]() =2
=2![]() ,∵CD2+BC2=(
,∵CD2+BC2=(![]() )2+(3
)2+(3![]() )2=20,BD2=(2
)2=20,BD2=(2![]() )2=20,∴CD2+BC2=BD2,∴△BCD是直角三角形;(3)y=﹣x2+2x+3对称轴为直线x=1.假设存在这样的点P,①以CD为底边,则P1D=P1C,设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,因此x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P1点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=
)2=20,∴CD2+BC2=BD2,∴△BCD是直角三角形;(3)y=﹣x2+2x+3对称轴为直线x=1.假设存在这样的点P,①以CD为底边,则P1D=P1C,设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,因此x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P1点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=![]() ,x2=
,x2=![]() <1,(不满足在对称轴右侧应舍去),∴x=
<1,(不满足在对称轴右侧应舍去),∴x=![]() ,∴y=4﹣x=
,∴y=4﹣x=![]() ,即点P1坐标为(
,即点P1坐标为(![]() ,
,![]() ).②以CD为一腰,∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,此时点P2坐标为(2,3).∴符合条件的点P坐标为(
).②以CD为一腰,∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,此时点P2坐标为(2,3).∴符合条件的点P坐标为(![]() ,
,![]() )或(2,3).
)或(2,3).


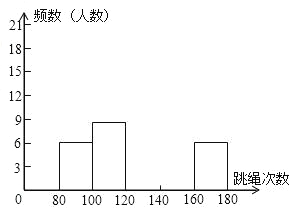
【题目】为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议: .
【题目】某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋的销量如下表所示:
尺码/厘米 | 22.5 | 23 | 23.5 | 24 | 24.5 |
销售量/双 | 35 | 40 | 30 | 17 | 8 |
通过分析上述数据,对鞋店业主的进货最有意义的是( )
A.平均数
B.众数
C.中位数
D.方差