题目内容
【题目】如图，△ABC是等腰直角三角形，∠ACB=90°，AB=4cm，动点P以1cm/s的速度分别从点A、B同时出发，点P沿A→B向终点B运动，点Q沿B→A向终点A运动，过点P作PD⊥AC于点D，以PD为边向右侧作正方形PDEF，过点Q作QG⊥AB，交折线BC﹣CA于点G与点C不重合，以QG为边作等腰直角△QGH，且点G为直角顶点，点C、H始终在QG的同侧，设正方形PDEF与△QGH重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜4）．
（1）当点F在边QH上时，求t的值；
（2）当正方形PDEF与△QGH重叠部分图形是四边形时，求S与t之间的函数关系式；
（3）当FH所在的直线平行或垂直于AB时，直接写出t的值．
【答案】
（1）
解：如图1中，当点F在边QH上时，易知AP=PQ=BQ，
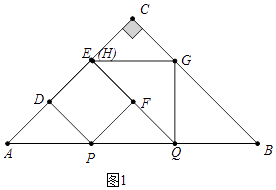
∵Rt△ABC中，AB=4，
∴t= 
时，点F在边QH上
（2）
解：如图2中，当点F在GQ上时，易知AP=BQ=t，PD=PF= 
t．PQ=PF= 
t，
∴t+ t+t=4，
∴t= 
，
由（1）可知，当 ＜t≤ 时，正方形PDEF与△QGH重叠部分图形是四边形
此时s= t[ t﹣ （4﹣2t）]= 
t2﹣2t．
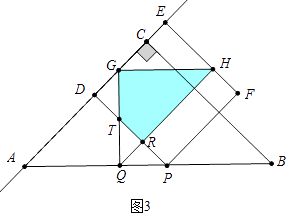
如图3中，当G在EF上时，则有 
（4﹣t）= t+ （2t﹣4）．解得t= 
，
如图4中，当G与D重合时，易知2t﹣4= t，解得t= 
．
当 ≤t＜ 时，S=S△GHQ﹣S△TRQ= （4﹣t）2﹣ [ 
（2t﹣4）]2=﹣ t2﹣4
（3）
解：①如图5中，当FH⊥AB时，延长HF交AB于T，易知AP=BQ=GQ=HG=TQ=t，PT= t，
∴3t+ t=4，
∴t= 
．
②如图7中，当HF⊥AB于T时，
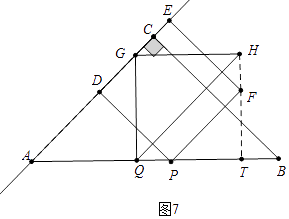
∵TB=4﹣2（4﹣t）=4﹣ t，解得t= 
，
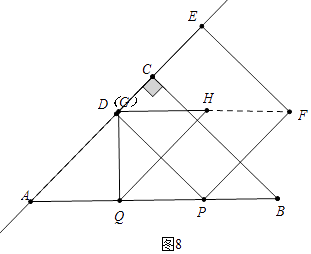
③如图8中，当HF∥AB时，∴ t+t=4，
∴t= ，
综上所述，t= s或 s或 时，FH所在的直线平行或垂直于AB
【解析】（1）如图1中，当点F在边QH上时，易知AP=PQ=BQ，求出AB的长即可解决问题；（2）分两种情形①如图2中，当点F在GQ上时，易知AP=BQ=t，PD=PF= t．PQ=PF= t，列出方程即可解决问题；②如图3中，重叠部分是四边形GHRT时；（3）分三种种情形求解①如图5中，当FH⊥AB时，延长HF交AB于T，易知AP=BQ=GQ=HG=TQ=t，PT= t；②如图7中，当FH∥AB时，易知AQ=PQ= t，BQ=t；分别列出方程即可解决问题．③如图8中，当HF∥AB时；
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．
