题目内容
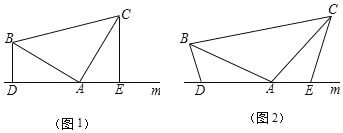
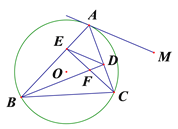
【题目】如图,△ABC是⊙O的内接三角形,CE⊥AB于点E,BD⊥AC于点D,BD、CE相交于点F,连结ED.
(1)若∠ABC=45°,证明AE=EF;
(2)求证:△AED∽△ACB;
(3)过点A的直线AM∥ED, AM是⊙O的切线吗?说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)是,证明见解析.
【解析】试题分析:(1)由ASA证明△BEF≌△CEA即可;
(2)先证明△AEC∽△ADB,得到AE:AD=AC:AB,再证明△AED∽△ACB即可;
(3)连接AO并延长交⊙O于N,连接NC.由△AED∽△ACB,得到∠ADE=∠ABC,由同弧所对的圆周角相等,得到∠ABC=∠N,等量代换得到∠ADE=∠N.由平行线的性质得到∠MAC=∠ADE,从而∠MAC=∠N.由AN为直径,得到∠CAN+∠N=90°,进而∠CAN+∠MAC=90°,即可得到结论.
试题解析:解:(1)∵∠ABC=45°,CE⊥AB,即∠BEC=90°,∴∠ECB=45°=∠EBC,∴EB=EC.
∵CE⊥AB,BD⊥AC,∴∠BEC=∠BDC=90°,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°.
∵∠EFB=∠DFC,∴∠EBF=∠DCF.
在△BEF和△CEA中,∵∠FBE=∠ACE,BE=CE,∠BEF=∠CEA=90°,∴△BEF≌△CEA,∴AE=EF.
(2)∵∠EBF=∠DCF,∠A=∠A,∴△AEC∽△ADB,∴AE:AD=AC:AB.∵∠A=∠A,∴△AED∽△ACB;
(3)AM是⊙O的切线.理由如下:
连接AO并延长交⊙O于N,连接NC.∵△AED∽△ACB,∴∠ADE=∠ABC.∵∠ABC=∠N,∴∠ADE=∠N.∵AM∥ED,∴∠MAC=∠ADE,∴∠MAC=∠N.∵AN为直径,∴∠NCA=90°,∴∠CAN+∠N=90°,∴∠CAN+∠MAC=90°,∴∠MAO=90°,∴AM是⊙O的切线.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某影院共有15排座位,第一排有12个座位数,从第2排开始,每一排都比前一排增加2个座位.
(1)请你在下表的空格里填写一个适当的式子.
第1排的座位数 | 第2排的座位数 | 第3排的座位数 | … | 第 |
12 | 14 | 16 | … |
(2)影院最后两排共有多少个座位?
【题目】体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图,如图:
次数 | 频数 |
| 2 |
| |
| 18 |
| 13 |
| 8 |
| |
| 1 |
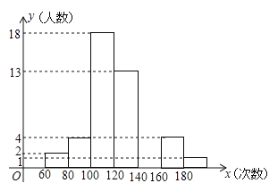
(1)补全频数分布表和频数分布直方图.
(2)上表中组距是__________次,组数是___________组.
(3)跳组次数在![]() 范围的学生有__________人,全班共有___________人.
范围的学生有__________人,全班共有___________人.
(4)若规定跳维次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?