题目内容
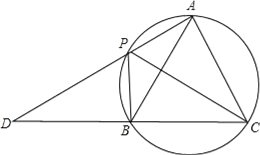
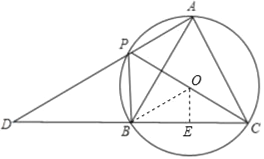
【题目】如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2![]()
①求PD的长.
②图中弧BP和线段DP、BD组成的图形面积为 (结果保留π)
【答案】(1)证明见解析;(2)①4;②3![]() ﹣
﹣![]() π.
π.
【解析】分析:(1)根据角平分线的定义结合∠APB=120°可得出∠BPC=60°,利用圆周角定理可求出∠BAC=60°,再根据圆内接四边形的性质可得出∠ACB=60°,由此即可证出△ABC是等边三角形;
(2)①通过解含30度角的直角三角形可求出AP、AD的长度,二者做差即可得出PD的长;
②根据圆内接四边形的性质找出∠PBC=90°,取PC的中点O,连接OB,过点O作OE⊥BC于点E,利用分割图形求面积法即可求出弧BP和线段DP、BD组成的图形面积.
本题解析:
(1)证明:∵∠APB=120°,PC平分∠APB,
∴∠BPC=∠APC=![]() ∠APB=60°,
∠APB=60°,
∴∠BAC=∠BPC=60°.
∵四边形APBC是圆内接四边形,∠APB=120°,
∴∠ACB=180°﹣∠APB=60°,
∴△ABC是等边三角形.
(2)解:①在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2![]() ,
,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4![]() ,AD=6,
,AD=6,
∴PD=AD﹣PA=4.
②∵∠PAC=90°,四边形APBC是圆内接四边形,
∴∠PBC=90°.
取PC的中点O,连接OB,过点O作OE⊥BC于点E,如图所示,
∴PO=![]() PC=2,OE=
PC=2,OE=![]() PB=
PB=![]() PA=1,
PA=1,
∴弧BP和线段DP、BD组成的图形面积=S△PCD﹣S△OBC﹣S扇形POB=![]() ×4
×4![]() ×2﹣
×2﹣![]() ×2
×2![]() ×1﹣
×1﹣![]() π×22=3
π×22=3![]() ﹣
﹣![]() π.
π.
故答案为:3![]() ﹣
﹣![]() π.
π.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案