题目内容
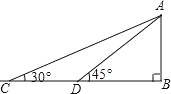
【题目】如图，某校数学兴趣小组为测得校园里旗杆AB的高度，在操场的平地上选择一点C，测得旗杆顶端A的仰角为30°，再向旗杆的方向前进16米，到达点D处（C、D、B三点在同一直线上），又测得旗杆顶端A的仰角为45°，请计算旗杆AB的高度（结果保留根号）
【答案】旗杆AB的高度是（8
+8）米．
【解析】
试题分析：根据锐角三角函数可得AB=CBtan30°，AB=BDtan45°，所以CBtan30°=BDtan45°，即（CD+DB）×
=BD×1，解得解得BD=8+8，由AB=BDtan45°即可求得旗杆AB的高度是（8+8）米．
根据题意可以得到BD的长度，从而可以求得AB的高度．
试题解析：由题意可得，
CD=16米，
∵AB=CBtan30°，AB=BDtan45°，
∴CBtan30°=BDtan45°，
∴（CD+DB）×=BD×1，
解得BD=8+8，
∴AB=BDtan45°=（8+8）米，
即旗杆AB的高度是（8+8）米．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
