题目内容
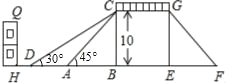
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,∠F=60°,求:
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

【答案】(1)旋转中心为点A,旋转角为90°;(2)DE=4![]() ﹣4,∠EBD=15°.
﹣4,∠EBD=15°.
【解析】
试题分析:(1)由于△ADF旋转一定角度后得到△ABE,根据旋转的性质得到旋转中心为点A,∠DAB等于旋转角,于是得到旋转角为90°;(2)根据旋转的性质得到AE=AF=4,∠AEB=∠F=60°,则∠ABE=90°﹣60°=30°,解直角三角形得到AD=4![]() ,∠ABD=45°,所以DE=4
,∠ABD=45°,所以DE=4![]() ﹣4,然后利用∠EBD=∠ABD﹣∠ABE计算即可.
﹣4,然后利用∠EBD=∠ABD﹣∠ABE计算即可.
试题解析:(1)∵△ADF旋转一定角度后得到△ABE,
∴旋转中心为点A,∠DAB等于旋转角,
∴旋转角为90°;
(2)∵△ADF以点A为旋转轴心,顺时针旋转90°后得到△ABE,
∴AE=AF=4,∠AEB=∠F=60°,
∴∠ABE=90°﹣60°=30°,
∵四边形ABCD为正方形,
∴AD=AB=4![]() ,∠ABD=45°,
,∠ABD=45°,
∴DE=4![]() ﹣4,
﹣4,
∠EBD=∠ABD﹣∠ABE=15°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目