Question

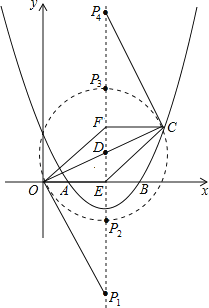
【题目】如图，抛物线y=ax2+bx+2与x轴交于点A（1，0）和B（4，0）．

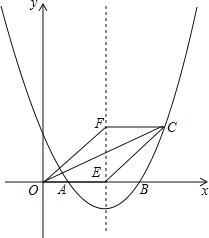
（1）求抛物线的解析式；

（2）若抛物线的对称轴交x轴于点E，点F是位于x轴上方对称轴上一点，FC∥x轴，与对称轴右侧的抛物线交于点C，且四边形OECF是平行四边形，求点C的坐标；

（3）在（2）的条件下，抛物线的对称轴上是否存在点P，使△OCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=x2﹣x+2；（2）（5，2）；（3）存在点P（，﹣）或（，）或（，）或（，）

【解析】

试题分析：方法一：

（1）把点A、B的坐标代入函数解析式，解方程组求出a、b的值，即可得解；

（2）根据抛物线解析式求出对称轴，再根据平行四边形的对角线互相平分求出点C的横坐标，然后代入函数解析式计算求出纵坐标，即可得解；

（3）设AC、EF的交点为D，根据点C的坐标写出点D的坐标，然后分①点O是直角顶点时，求出△OED和△PEO相似，根据相似三角形对应边成比例求出PE，然后写出点P的坐标即可；②点C是直角顶点时，同理求出PF，再求出PE，然后写出点P的坐标即可；③点P是直角顶点时，利用勾股定理列式求出OC，然后根据直角三角形斜边上的中线等于斜边的一半可得PD=OC，再分点P在OC的上方与下方两种情况写出点P的坐标即可．

方法二：

（1）略．

（2）因为四边形OECF是平行四边形，且FC∥x轴，列出F，C的参数坐标，利用FC=OE，可求出C点坐标．

（3）列出点P的参数坐标，分别列出O，C两点坐标，由于△OCP是直角三角形，所以分别讨论三种垂直的位置关系，利用斜率垂直公式，可求出三种情况下点P的坐标．

方法一：

解：（1）把点A（1，0）和B（4，0）代入y=ax2+bx+2得，

，

解得，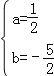

所以，抛物线的解析式为y=x2﹣x+2；

（2）抛物线的对称轴为直线x=，

∵四边形OECF是平行四边形，

∴点C的横坐标是×2=5，

∵点C在抛物线上，

∴y=×52﹣×5+2=2，

∴点C的坐标为（5，2）；

（3）设OC与EF的交点为D，

∵点C的坐标为（5，2），

∴点D的坐标为（，1），

①点O是直角顶点时，易得△OED∽△PEO，

∴=，

即=，

解得PE=，

所以，点P的坐标为（，﹣）；

②点C是直角顶点时，同理求出PF=，

所以，PE=+2=，

所以，点P的坐标为（，）；

③点P是直角顶点时，由勾股定理得，OC==，

∵PD是OC边上的中线，

∴PD=OC=，

若点P在OC上方，则PE=PD+DE=+1，

此时，点P的坐标为（，），

若点P在OC的下方，则PE=PD﹣DE=﹣1，

此时，点P的坐标为（，），

综上所述，抛物线的对称轴上存在点P（，﹣）或（，）或（，）或（，），使△OCP是直角三角形．

方法二：

（1）略．

（2）∵FC∥x轴，∴当FC=OE时，四边形OECF是平行四边形．

设C（t，），

∴F（，+2），

∴t﹣=，

∴t=5，C（5，2）．

（3）∵点P在抛物线的对称轴上，设P（，t），O（0，0），C（5，2），

∵△OCP是直角三角形，∴OC⊥OP，OC⊥PC，OP⊥PC，

①OC⊥OP，∴KOC×KOP=﹣1，∴，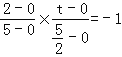

∴t=﹣，∴P（，﹣），

②OC⊥PC，∴KOC×KPC=﹣1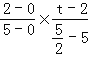，∴=﹣1，

∴t=，P（，），

③OP⊥PC，∴KOP×KPC=﹣1，∴，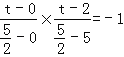

∴4t2﹣8t﹣25=0，∴t=或，

点P的坐标为（，）或（，），

综上所述，抛物线的对称轴上存在点P（，﹣）或（，）或（，）或（，），使△OCP是直角三角形．