题目内容
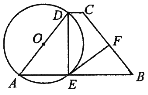
【题目】如图,Rt△ACB中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
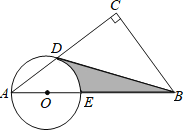
(1)判断BD所在直线与⊙O的位置关系,并证明你的结论;
(2)若AE=4,∠A=30°,求图中由BD、BE、弧DE围成阴影部分面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,DE,求出∠ADE=90°=∠C,推出DE∥BC,求出∠EDB=∠CBD=∠A,根据∠A+∠OED=90°,求出∠EDB+∠ODE=90°,根据切线的判定推出即可;
(2)分别求出扇形DOE和△ODB的面积,即可求出答案.
解:(1)直线BD与⊙O的位置关系是相切
证明:连接OD、DE

∵∠C=90°
∴∠CBD+∠CDB=90°
∵∠A=∠CBD
∴∠A+∠CDB=90°
∵OD=OA
∴∠A=∠ADO
∴∠ADO+∠CDB=90°
∴∠ODB=180°﹣90°=90°
∴OD⊥BD
∵OD为半径
∴BD是⊙O切线
(2)解:∵AE是⊙O直径
∴∠ADE=90°
∵AE=4,∠A=30°
∴DE=![]() AE=2,∠AED=60°
AE=2,∠AED=60°
∵OD=OE
∴△DOE是等边三角形
∴∠ODE=60°,OD=OE=DE=2
∵∠ODB=90°
∴∠EDB=30°
∴∠B=∠DEO﹣∠EDB=60°﹣30°=30°
∴OB=2OD=4
由勾股定理得:DB=![]() ,
,
∴阴影部分的面积S=S△ODB﹣S扇形DOE
=![]()
=![]() .
.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目