题目内容
【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣4,0),B(1,0),交y轴于C点,且OC=2OB.
(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标.
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
【答案】
(1)解:∵B(1,0),OC=2OB,
∴C(0,﹣2),
设抛物线解析式为y=a(x+4)(x﹣1),
把C(0,﹣2)代入得a4(﹣1)=﹣2,解得a= ![]() ,
,
∴抛物线的解析式为y= ![]() (x+4)(x﹣1),即y=
(x+4)(x﹣1),即y= ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)解:AB=1﹣(﹣4)=5,
设直线BC的解析式为:y=kx+b,
把B(1,0),C(0,﹣2)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=2x﹣2,
设D(m,2m﹣2),
∵△ABD为以AB为腰的等腰三角形,
∴BD=BA=5或AD=AB=5,
当BD=BA时,即(m﹣1)2+(2m﹣2)2=52,解得m1=1+ ![]() ,m2=1﹣
,m2=1﹣ ![]() ,此时D点坐标为(1+
,此时D点坐标为(1+ ![]() ,2
,2 ![]() ),(1﹣
),(1﹣ ![]() ,﹣2
,﹣2 ![]() ),
),
当AD=AB时,即(m+4)2+(2m﹣2)2=52,解得m1=1(舍去),m2=﹣1,此时D点坐标为(﹣1,﹣4),
综上所述,满足条件的D点坐标为(1+ ![]() ,2
,2 ![]() ),(1﹣
),(1﹣ ![]() ,﹣2
,﹣2 ![]() ),(﹣1,﹣4)
),(﹣1,﹣4)
(3)解:AB2=25,BC2=12+22=5,AC2=42+22=20,
∵AB2=BC2+AC2,
∴△ABC为直角三角形,∠ACB=90°,
∵∠BAC=∠CAO,
∴△ACO∽△ABC,
∵△APQ与△ABC相似,
∴∠CAP=∠OAC,
∴AC平分∠BAP,
设直线AP交y轴于E,作CF⊥AE于F,
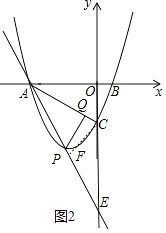
则CF=CO=2,
∵∠CEF=∠AEO,
∴△ECF∽△EAO,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
在Rt△AOE中,∵OE2+OA2=AE2,
∴(2+CE)2+42![]() ,
,
∴E(0,﹣ ![]() ),
),
设直线AE的解析式为y=mx+n,
把A(﹣4,0),E(0,﹣ ![]() )得
)得 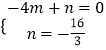 ,解得
,解得 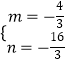 ,
,
∴直线AE的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
解方程组 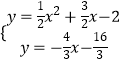 ,解得
,解得 ![]() 或
或 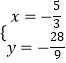 ,
,
∴P(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】根据OC=2OB.及点B的坐标就可以求出点C的坐标,注意:点C在y轴的负半轴,A、B两点坐标是此抛物线与x轴的两交点坐标,因此设函数解析式为两根式,代入点的坐标即可求出此抛物线的函数解析式。
(2)先求出AB的长及直线BC的函数解析式,抓住点D在直线BC上,设出点D的坐标,是以AB为腰的等腰三角形。再分类讨论。当BD=BA时和当AD=AB时,建立方程求解,即可求出满足条件的点D的坐标。
(3)要求点p的坐标,点P是直线AP与抛物线的交点坐标,解决此题的关键就是要求出直线AP的函数解析式。因此设直线AP交y轴于E,作CF⊥AE于F,,求出点E的坐标即可。根据已知条件易得到 △ ABC是直角三角形,从而得到△ACO∽△ABC,由△APQ与△ABC相似,得出AC平分∠BAP。根据角平分线的性质,得到CF=CO,再证明△ECF∽△EAO,求出CE和AE的数量关系,根据勾股定理就可以求出CE的长,即可得到点E的坐标,即可求出直线AE的解析式,再求出两函数图像的交点坐标即可得出结果。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.






