题目内容
设a＞b＞0，a2+b2=4ab，则
的值等于 ．
【答案】分析：由a2+b2=4ab，先求出（a+b）和（a-b）的平方，进而求出（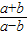
）2=3，然后再求算术平方根．
解答：解：由a2+b2=4ab，可得：
（a+b）2=6ab----（1）；
（a-b）2=2ab---（2）；
（1）÷（2）得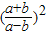
=3，
∵a＞b＞0，∴a-b＞0，
即
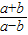＞0，
故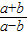
=
．
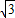点评：此题有一定难度，考查了完全平方公式的灵活应用，熟练掌握公式并灵活运用是解题的关键．
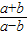）2=3，然后再求算术平方根．解答：解：由a2+b2=4ab，可得：
（a+b）2=6ab----（1）；
（a-b）2=2ab---（2）；
（1）÷（2）得
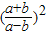=3，∵a＞b＞0，∴a-b＞0，
即
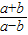＞0，故
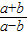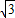=．点评：此题有一定难度，考查了完全平方公式的灵活应用，熟练掌握公式并灵活运用是解题的关键．
练习册系列答案
相关题目