题目内容
已知:如图,AB为⊙O的弦,OD⊥AB,垂足为点D,DO的延长线交⊙O于点C.过点C作CE⊥AO,分别与AB、AO的延长线相交于E、F两点.CD = 8, .
.

求:(1)弦AB的长;
(2)△CDE的面积.
 .
.
求:(1)弦AB的长;
(2)△CDE的面积.
(1)8(2)24
解:(1)设⊙O的半径OA = r,那么OD =" 8" –r.
由 OD⊥AB,得 ∠ADO = 90°.
于是,由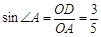 ,即得
,即得 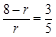 .
.
解得 r = 5.……………………………………………………………(2分)
∴ OA = 5,OD = 3.
利用勾股定理,得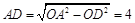 .………………………(2分)
.………………………(2分)
∵ OD⊥AB,O为圆心,∴ AB = 2AD = 8.………………………(1分)
(2)∵ CE⊥AO,∴ ∠AFE =∠CDE = 90°.
于是,由 ∠A +∠AEF = 90°,∠C +∠CED = 90°,
得 ∠A =∠C.…………………………………………………………(1分)
又∵ ∠ADO =∠CDE = 90°,
∴ △AOD∽△CED.
∴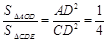 .………………………………………………(2分)
.………………………………………………(2分)
∵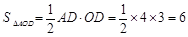 ,
,
∴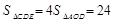 .………………………………………………(2分)
.………………………………………………(2分)
(1)设圆的半径为r,则OD =" 8" –r.利用三角函数和勾股定理求解;
(2)证得△AOD∽△CED,得出面积之比等于相似比的平方。
由 OD⊥AB,得 ∠ADO = 90°.
于是,由
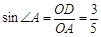 ,即得
,即得 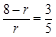 .
.解得 r = 5.……………………………………………………………(2分)
∴ OA = 5,OD = 3.
利用勾股定理,得
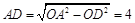 .………………………(2分)
.………………………(2分)∵ OD⊥AB,O为圆心,∴ AB = 2AD = 8.………………………(1分)
(2)∵ CE⊥AO,∴ ∠AFE =∠CDE = 90°.
于是,由 ∠A +∠AEF = 90°,∠C +∠CED = 90°,
得 ∠A =∠C.…………………………………………………………(1分)
又∵ ∠ADO =∠CDE = 90°,
∴ △AOD∽△CED.
∴
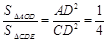 .………………………………………………(2分)
.………………………………………………(2分)∵
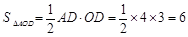 ,
,∴
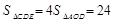 .………………………………………………(2分)
.………………………………………………(2分)(1)设圆的半径为r,则OD =" 8" –r.利用三角函数和勾股定理求解;
(2)证得△AOD∽△CED,得出面积之比等于相似比的平方。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
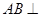 半径
半径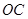 于
于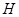 ,
,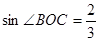 ,则
,则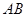 的长度为
的长度为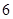
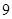
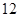
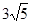
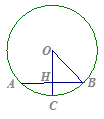
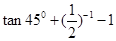 .
. 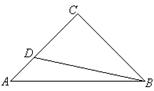
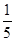 ,则sin∠CBD值为
,则sin∠CBD值为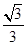 B.
B.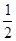
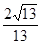 D.
D.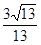
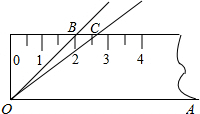
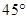 的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将
的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将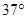 的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm
的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm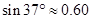 ,
,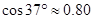 ,
,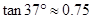 )
)
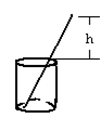
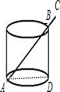
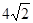 ,则可知大圆半径是(▲).
,则可知大圆半径是(▲). 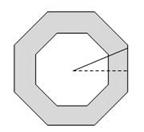
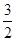
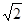
 中,
中,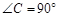 ,若
,若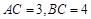 ,则
,则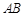 的值为( )
的值为( )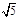
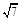
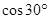 = .
= .