题目内容
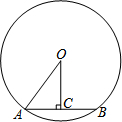 如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,cosA=
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,cosA=| 3 |
| 5 |
(1)求OC的长;
(2)点E,F在⊙O上,EF∥AB.若EF=16,直接写出EF与AB之间的距离.
考点:垂径定理,勾股定理,解直角三角形
专题:
分析:(1)由垂径定理求得AC=6;然后通过解Rt△AOC来求OC的长度;
(2)需要分类讨论:EF在圆心是下方和EF在圆心的上方两种情况.
(2)需要分类讨论:EF在圆心是下方和EF在圆心的上方两种情况.
解答: 解:(1)∵AB是⊙O的弦,OC⊥AB于C,AB=12,
解:(1)∵AB是⊙O的弦,OC⊥AB于C,AB=12,
∴AC=
AB=6.
∵在Rt△AOC中,∠ACO=90°,cosA=
,
∴OA=10,
∴OC=
=8;
(2)设直线CO交EF于点D,连接OE.
∵EF∥AB,
∴OD⊥EF,ED=
EF=8.
∴在直角△OED中,根据勾股定理得到:OD=
=
=6.
如图1,CD=OC-OD=8-6=2;
如图2,CD=OC,+OD=8+6=14;
综上所述,EF与AB之间的距离是2或14.
 解:(1)∵AB是⊙O的弦,OC⊥AB于C,AB=12,
解:(1)∵AB是⊙O的弦,OC⊥AB于C,AB=12,∴AC=
| 1 |
| 2 |
∵在Rt△AOC中,∠ACO=90°,cosA=
| 3 |
| 5 |
∴OA=10,
∴OC=
| OA2-AC2 |
(2)设直线CO交EF于点D,连接OE.
∵EF∥AB,
∴OD⊥EF,ED=
| 1 |
| 2 |
∴在直角△OED中,根据勾股定理得到:OD=
| OE2-ED2 |
| 102-82 |
如图1,CD=OC-OD=8-6=2;
如图2,CD=OC,+OD=8+6=14;
综上所述,EF与AB之间的距离是2或14.
点评:本题考查了解直角三角形,勾股定理和垂径定理.解(2)题时,要分类讨论,不要漏解.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
若两个圆的半径分别为2和1,圆心距为3,则这两个圆的位置关系是( )
| A、内含 | B、内切 | C、相交 | D、外切 |
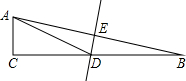 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC与D,交AB于E.若BD=12,则AC=
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC与D,交AB于E.若BD=12,则AC=
 如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到0.1m,参考数据:
如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到0.1m,参考数据: 二次函数y=-x2+bx+c的部分图象如图所示,图象的对称轴为过点(-1,0)且平行于y轴的直线,图象与x轴交于点(1,0),则一元二次方程-x2+bx+c=0的根为
二次函数y=-x2+bx+c的部分图象如图所示,图象的对称轴为过点(-1,0)且平行于y轴的直线,图象与x轴交于点(1,0),则一元二次方程-x2+bx+c=0的根为 如图,圆柱形水管内积水的水面宽度AB=8cm、C为弧AB的中点,圆柱形水管的截面内半径为5cm,则此时水深CD的值为
如图,圆柱形水管内积水的水面宽度AB=8cm、C为弧AB的中点,圆柱形水管的截面内半径为5cm,则此时水深CD的值为 如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E.阴影部分面积为
如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E.阴影部分面积为