题目内容
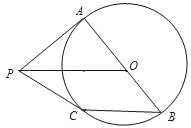
【题目】如图,PA,PB是⊙O的切线,A,B为切点,点C在PB上,OC∥AP,CD⊥AP于点D.
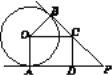
(1)求证:OC=AD;
(2)若∠P=50°,⊙O的半径为4,求四边形AOCD的周长(精确到0.1,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).
【答案】(1)证明见解析(2)18.4
【解析】
(1)、根据切线的性质得出OA⊥PA,结合已知条件证明出四边形AOCD为矩形,从而得出答案;(2)、根据Rt△OBC中∠BCO的正弦值得出OC的长度,从而得出四边形的周长.
(1)证明:∵PA切⊙O于点A, ∴OA⊥PA,即∠OAD=90°,∵OC∥AP,
∴∠COA=180°-∠OAD=180°-90°=90°, ∵CD⊥AP,∴∠CDA=∠OAD=∠COA=90°,
∴四边形AOCD是矩形,∴OC=AD;
(2)∵PB切⊙O于点B,∴∠OBP=90°, ∵OC∥AP,∴∠BCO=∠P=50°,
在Rt△OBC中,sin∠BCO=![]() ,OB=4, ∴OC=
,OB=4, ∴OC=![]() ≈5.22,
≈5.22,
∴四边形AOCD的周长为2(OA+OC)≈2×(4+5.22)≈18.4.

练习册系列答案
相关题目