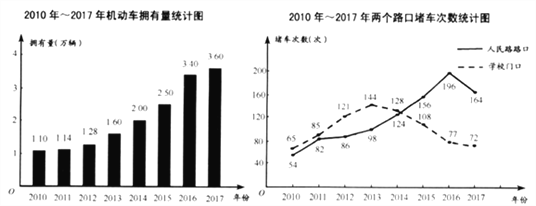
题目内容
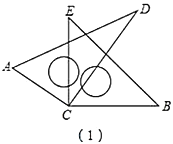
【题目】如图,已知△ABC和△DEC都是等腰直角三角形,![]() ,
,![]() 连接AE.
连接AE.
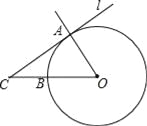
(1)如图(1),点D在BC边上,连接AD,ED延长线交AD于点F,若AB=4,求△ADE的面积
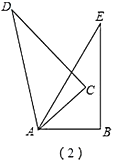
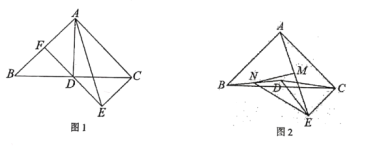
(2)如图2,点D在△ABC的内部,点M是AE的中点,连接BD,点N是BD中点,连接MN,NE,求证![]() 且
且![]() .
.
【答案】(1)2;(2)证明见详解.
【解析】
(1)由等腰直角三角形的性质,即可得到CE=DE=AF=![]() ,然后根据面积公式即可得到答案;
,然后根据面积公式即可得到答案;
(2)如图2中,延长EN至F使NF=NE,连接AF、BF,先证明△DNE≌△BNF,再证明△ABF≌△ACE,推出∠FAB=∠EAC,可得∠FAE=∠FAB+∠BAE=∠BAE+∠EAC=90°,由此即可解决问题.
解:(1)∵△ABC和△DEC都是等腰直角三角形,![]()
∴AB=AC,DE=EC,∠B=∠ACB=∠EDC=∠ECD=45°,
∵![]() ,
,
∴AD⊥BC,
∴△ABD是等腰直角三角形,
∴AF=![]() ,
,
∵![]()
∴四边形AFEC是矩形,
∴CE=AF=DE=2,
∴![]() ;
;
(2)如图2中,延长EN至F使NF=NE,连接AF、BF.
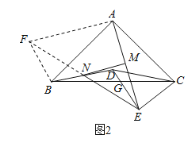
在△DNE和△BNF中,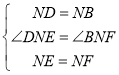 ,
,
∴△DNE≌△BNF,
∴BF=DE=EC,∠FBN=∠EDN,
∵∠ACB=∠DCE=45°,
∴∠ACE=90°-∠DCB,
∴∠ABF=∠FBN-∠ABN
=∠BDE-∠ABN
=180°-∠DBC-∠DGB-∠ABN
=180°-∠DBC-∠DCB-∠CDE-∠ABN
=180°-(∠DBC+∠ABN)-∠DCB-45°
=180°-45°-45°-∠DCB=90°-∠DCB=∠ACE,
在△ABF和△ACE中,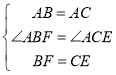 ,
,
∴△ABF≌△ACE.
∴∠FAB=∠EAC,AE=AF
∴∠FAE=∠FAB+∠BAE=∠BAE+∠EAC=90°,
∵N为FE中点,M为AE中点,
∴AF∥NM,MN=![]() AF,ME=
AF,ME=![]() AE
AE
∴MN⊥AE,MN=ME.
即![]() 且
且![]() .
.

 阅读快车系列答案
阅读快车系列答案