题目内容
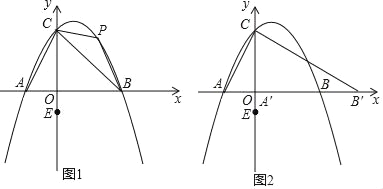
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在x轴上是否存在点E,使以点B,C,E为顶点的三角形为等腰三角形?如果存在,直接写出E点坐标;如果不存在,请说明理由.

【答案】(1)y=﹣x2+3x+4;(2)m=﹣t2+4t(0<t<4),m的最大值为4;(3)存在,E(﹣4,0)或(0,0)或(4﹣4![]() ,0).
,0).
【解析】
(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式;
(2)将x=0代入抛物线解析式中可求出点C的坐标,根据点B、C的坐标利用待定系数法即可求出直线BC的解析式,由点P的横坐标为t,即可找出点P、Q的坐标,由此即可用含t的代数式表示出PQ的长度,再利用二次函数的性质即可解决最值问题;
(3)①由CO⊥x轴、QD⊥x轴、∠QBD=∠CBO,即可得出△BQD∽△BCO,即存在点E(0,0)使得△BQD∽△BCE;②过点C作EC⊥BC交x轴于点E,由EC⊥BC、QD⊥x轴、∠QBD=∠CBO,即可得出△BQD∽△BEC,再根据点B、C的坐标即可得出∠CBO=45°,利用等腰直角三角形的性质即可得出此时点E的坐标.综上即可得出结论.
(1)∵抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0),
把A、B两点坐标代入上式,解得:a=﹣1,c=4,
故:抛物线y=﹣x2+3x+4;
(2)∵将x=0代入抛物线的解析式得:y=4,∴C(0,4),
把将B(4,0),C(0,4)代入抛物线方程,
解得:直线BC的解析式为:y=﹣x+4.
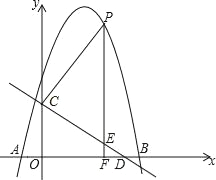
过点P作x的垂线PQ,如图所示:
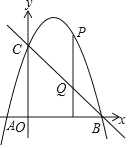
∵点P的横坐标为t,∴P(t,﹣t2+3t+4),Q(t,﹣t+4).
∴PQ=﹣t2+3t+4﹣(﹣t+4)=﹣t2+4t.
∴m=﹣t2+4t=﹣(t﹣2)2+4(0<t<4).
∴当t=2时,m的最大值为4;
(3)存在.如图所示:
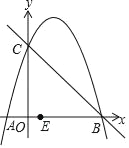
当EC=BE时,E在原点O,此时点E(0,0),
当BC=CE时,E在点B关于y轴对称点,此时点E(﹣4,0),
当BC=BE时,BE=4![]() ,此时E(4﹣4
,此时E(4﹣4![]() ,0)
,0)
即:E(﹣4.0)或(0,0)或(4﹣4![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.