题目内容
 如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:(1)旋转中心是
点O
点O
,旋转角是∠BOD或∠AOC
∠BOD或∠AOC
.(2)经过旋转,点A、B分别移到了
C、D
C、D
.(3)若AO=3cm,则CO=
3cm
3cm
.(4)若∠AOC=60°,∠AOD=20°,则∠BOD=
60°
60°
,∠DOC=40°
40°
.分析:(1)根据旋转的性质,对应边BO、DO的交点即为旋转中心,夹角为旋转角;
(2)结合图形找出A、B的对应点即可;
(3)根据旋转变换只改变图形的位置不改变图形的形状与大小可得CO=AO;
(4)根据∠AOC、∠BOD都等于旋转角解答,再根据∠DOC=∠AOC-∠AOD代入数据进行计算即可得解;
(2)结合图形找出A、B的对应点即可;
(3)根据旋转变换只改变图形的位置不改变图形的形状与大小可得CO=AO;
(4)根据∠AOC、∠BOD都等于旋转角解答,再根据∠DOC=∠AOC-∠AOD代入数据进行计算即可得解;
解答:解:(1)旋转中心是点O,旋转角是∠BOD或∠AOC;
(2)经过旋转,点A、B分别移到了C、D;
(3)∵AO=3cm,
∴CO=AO=3cm;
(4)∵∠AOC=60°,
∴∠BOD=∠AOC=60°,
∠DOC=∠AOC-∠AOD=60°-20°=40°.
故答案为:(1)点O,∠BOD或∠AOC;(2)C、D;(3)3cm;(4)60°,40°.
(2)经过旋转,点A、B分别移到了C、D;
(3)∵AO=3cm,
∴CO=AO=3cm;
(4)∵∠AOC=60°,
∴∠BOD=∠AOC=60°,
∠DOC=∠AOC-∠AOD=60°-20°=40°.
故答案为:(1)点O,∠BOD或∠AOC;(2)C、D;(3)3cm;(4)60°,40°.
点评:本题考查了旋转的性质,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图所示,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图所示,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
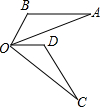 如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中: