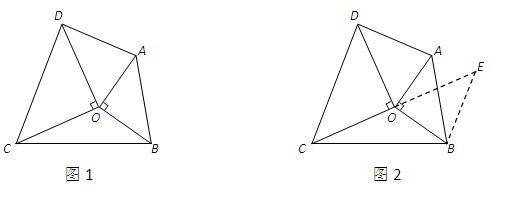题目内容
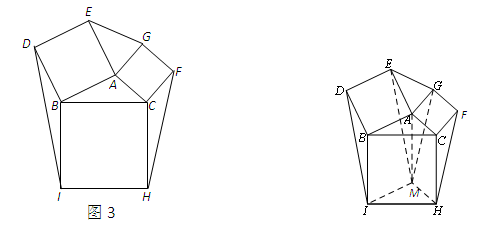
如图1:△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90°. 将△AOD绕点O顺时针旋转90°得△OBE,从而构造出以AD、BC、OC+OD的长度为三边长的△BCE(如图2).若△BOC的面积为1,则△BCE面积等于___________.
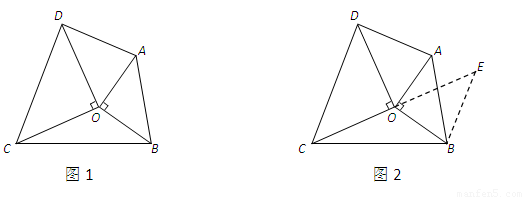
如图3,已知△ABC,分别以AB、AC、BC为边向外作正方形ABDE、AGFC、BCHI,连接EG、FH、ID.
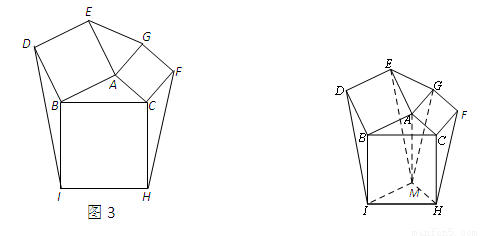
①在图3中利用图形变换画出并指明以EG、FH、ID的长度为三边长的一个三角形(保留作图痕迹);
②若△ABC的面积为1,则以EG、FH、ID的长度为三边长的三角形的面积等于____
【答案】
2,△EGM,3
【解析】∵△CDO为等腰直角三角形,∴CO=DO, ∵OE=OD∴CO=OE∴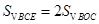 =2.
=2.
①利用平行四边形的性质把FH、ID平移到以EG为一边的三角形中来;
②根据图2的得出的结论是△ABC与△BID、△AEG、△CFH面积相等,而所作的三角形面积又等于△BID、△AEG、△CFH面积之和,所以以EG、FH、ID的长度为三边长的三角形的面积等于3.

练习册系列答案
相关题目