题目内容
【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .
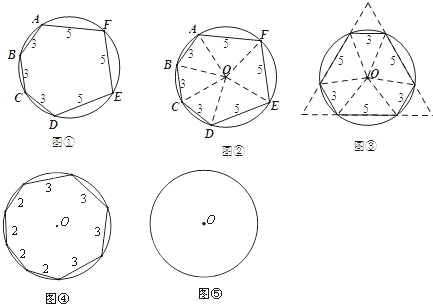
(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
【答案】(1)![]() (2)13+12
(2)13+12![]() .
.
【解析】
试题分析:(1)如图③,利用六边形ABCDEF每次绕圆心O旋转120°都和原来的图形重合可判断△MNQ为等边三角形,△MAF、△NBC和△QDE都是等边三角形,然后根据等边三角形的面积公式求解;
(2)先画出分割重组的图形,如图⑤,利用八边形ABCDEFGH为轴对称图形,每次绕圆心O旋转90°都和原来的图形重合,可判断四边形PQMN为正方形,△PAB、△GCD、△MEF、△NHG都是等腰直角三角形,根据根据正方形的性质和等腰直角三角形的性质求解.
试题解析:(1)如图③,∵六边形ABCDEF为轴对称图形,每次绕圆心O旋转120°都和原来的图形重合,∴△MNQ为等边三角形,△MAF、△NBC和△QDE都是等边三角形,
∴NQ=3+5+3=11,
∴六边形ABCDEF的面积=S△MNQ﹣3S△AMN
=![]() ×112﹣3×
×112﹣3×![]() ×32
×32
=![]() ;
;
故答案为![]() .
.
(2)如图⑤,∵八边形ABCDEFGH为轴对称图形,每次绕圆心O旋转90°都和原来的图形重合,
∴四边形PQMN为正方形,△PAB、△GCD、△MEF、△NHG都是等腰直角三角形,
∴PA=![]() AB=
AB=![]() ,PN=
,PN=![]() +3+
+3+![]() =3+2
=3+2![]() ,
,
∴这个八边形的面积=(3+2![]() )2﹣4×
)2﹣4×![]() ×
×![]() ×
×![]() =9+12
=9+12![]() +8﹣4=13+12
+8﹣4=13+12![]() .
.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案