题目内容
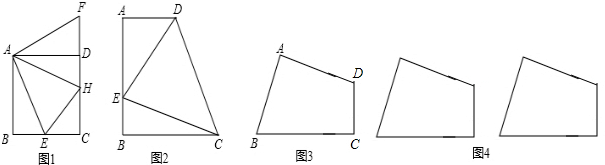
如图1,在正方形ABCD的边AB上取一点P(不与端点A,B重合),以AP为一边作正方形APEF,连接BE,DE,观察图形,有如下三个结论成立:①BE=DE;②BP=DF;③BP⊥DF.如图2,将正方形APEF绕点A逆时针旋转,旋转角为α(0°<α<90°).(1)旋转后,上述三个结论仍然成立的有哪些?写出仍然成立的结论,并证明;
(2)若正方形APEF的边长为2
| 3 |
分析:(1)由图观察,旋转后依然成立的结论应该是②和③,连接BP,DF,BP的延长线分别交AD,DF于点M,N.要证明BP⊥DF,就要证明∠FDA+∠DMN=90°,∠DMN=∠AMB.
而∠AMB+∠ABM=90°,因此要证BP⊥DF,就要证明∠FDA=∠ABM.
我们发现要证明的∠FDA=∠ABM和BP=DF都在三角形ADF和ABP中,那么只要证明△ADF和△ABP全等即可.
因为∠DAF和∠PAB都与∠DAP互余,因此∠DAF=∠PAB,又有AP=AF,AB=AD.因此两三角形就全等了.
(2)分两种情况:①G在EF边上;②G在EP边上解答.
而∠AMB+∠ABM=90°,因此要证BP⊥DF,就要证明∠FDA=∠ABM.
我们发现要证明的∠FDA=∠ABM和BP=DF都在三角形ADF和ABP中,那么只要证明△ADF和△ABP全等即可.
因为∠DAF和∠PAB都与∠DAP互余,因此∠DAF=∠PAB,又有AP=AF,AB=AD.因此两三角形就全等了.
(2)分两种情况:①G在EF边上;②G在EP边上解答.
解答:解:(1)旋转后,仍然成立的结论是:②BP=DF,③BP⊥DF.
证明:连接BP,DF,
∵∠PAB=α=90°-∠DAP=∠FAD,
AP=AF,AB=AD,
∴△ABP≌△ADF,
∴BP=DF,
延长BP,分别交AD,DF于点M,N,
由△ABP≌△ADF得∠MBA=∠MDN,
又∠BMA=∠DMN,
∴∠DNM=∠BAD=90°,即BP⊥DF.

(2)分两种情况:①当G在EF边上时,如备用图.
在直角三角形FGA中,cos∠FAG=AF:AG=
:2,因此∠FAG=30°.
因此,∠GAP=60°,∠PAB=∠α=30°.
②当G在EP边上时,如图2.
求法同①只不过是在直角三角形GAP中进行求值,求出的结果是∠PAB=∠α=60°.
故旋转角α的度数为30°或60°.
证明:连接BP,DF,
∵∠PAB=α=90°-∠DAP=∠FAD,
AP=AF,AB=AD,
∴△ABP≌△ADF,
∴BP=DF,
延长BP,分别交AD,DF于点M,N,
由△ABP≌△ADF得∠MBA=∠MDN,
又∠BMA=∠DMN,
∴∠DNM=∠BAD=90°,即BP⊥DF.

(2)分两种情况:①当G在EF边上时,如备用图.
在直角三角形FGA中,cos∠FAG=AF:AG=
| 3 |
因此,∠GAP=60°,∠PAB=∠α=30°.
②当G在EP边上时,如图2.
求法同①只不过是在直角三角形GAP中进行求值,求出的结果是∠PAB=∠α=60°.
故旋转角α的度数为30°或60°.
点评:平移、翻折和旋转是初中几何重要的三种变换方式,变换之后的几何图形与原图形对应的边、角均相等.巧妙地运用变换的基本性质或构造变换图形,均可以使题目的解答简易而顺畅.

练习册系列答案
相关题目

 构造一个与上述命题类似的正确命题并加以证明.
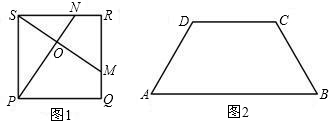
构造一个与上述命题类似的正确命题并加以证明. 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.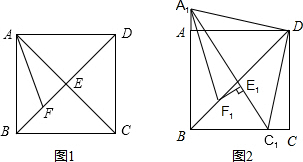 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.