题目内容
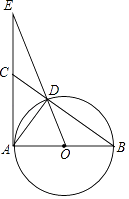
【题目】已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有 . ①∠B=∠CAD;②点C是AE的中点;③ ![]() =
= ![]() ;④tan B=
;④tan B= ![]() .
.
【答案】①③④
【解析】解:∵AB为直径, ∴∠ADB=90°,
∴∠B+∠DAB=90°,
∵∠CAD+∠DAB=90°,
∴∠B=∠CAD,故①正确;
∵∠CAD=∠B=∠ODB=∠CDE,∠E=∠E,
∴△ECD∽△EDA,
∴ ![]() =
= ![]() ,
,
∵OA=1,AE=3,
∴OE= ![]() ,ED=
,ED= ![]() ﹣1,
﹣1,
∴ ![]() =
= ![]() ,
,
∴CE= ![]() ≠
≠ ![]() AE,
AE,
即点C不是AE的中点,故②不正确;
由△ECD∽△EDA,得 ![]() =
= ![]() ,
,
在Rt△ABC中,AD⊥BC,
∴△ACD∽△BAD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,故③正确;
,故③正确;
tanB= ![]() =
= ![]() =
= ![]() =
= ![]() ,故④正确.
,故④正确.
所以答案是:①③④.
【考点精析】利用圆周角定理和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩(m) | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
次数 | 1 | 1 | 2 | 5 | 1 |
则下列关于这组数据的说法中正确的是( )
A.众数是2.45
B.平均数是2.45
C.中位数是2.5
D.方差是0.48