题目内容
如图,直线y=2x+2与x轴,y轴分别交于A、B两点,点C是在第一象限内此直线上的一个动点,以BC为直角边作如图 所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
(1)找出图中一对相似三角形(不再标记字母),并说明理由;
(2)在C的运动过程中,DE的长度是否改变?若不变,请求出DE的长;若变化,请说明理由.
 所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.(1)找出图中一对相似三角形(不再标记字母),并说明理由;
(2)在C的运动过程中,DE的长度是否改变?若不变,请求出DE的长;若变化,请说明理由.
分析:(1)根据圆周角定理,同弧所对的圆周角相等,即可的到BAD=∠DEC,根据三角形外角的性质得出∠ABD=∠EDC,从而得到△ABD∽△EDC;
(2)根据相似三角形的对应边的比相等即可求解.
(2)根据相似三角形的对应边的比相等即可求解.
解答:解:(1)连接AC.
∵∠BAD与∠DEC是同弧所对的圆周角,
∴∠BAD=∠DEC,
∵△BCD是等腰直角三角形,
∴∠DBC=∠BDC=45°,∠ABD=180°-45°=135°,
∵DE⊥BD,
∴∠ADE=90°,
∴∠EDC=∠BDC+∠BDE=45°+90°=135°,
∴∠ABD=∠EDC,
∴△ABD∽△EDC;
(2)DE的长度不变.
AB=
,
∵△ABD∽△EDC,
∴
=
,则DE=
AB=
.
∵∠BAD与∠DEC是同弧所对的圆周角,
∴∠BAD=∠DEC,
∵△BCD是等腰直角三角形,
∴∠DBC=∠BDC=45°,∠ABD=180°-45°=135°,
∵DE⊥BD,
∴∠ADE=90°,
∴∠EDC=∠BDC+∠BDE=45°+90°=135°,
∴∠ABD=∠EDC,
∴△ABD∽△EDC;
(2)DE的长度不变.
AB=
| 5 |
∵△ABD∽△EDC,
∴
| DE |
| AB |
| DC |
| BD |
| ||
| 2 |
| ||
| 2 |
点评:本题是圆周角定理与相似三角形的判定与性质的综合应用,正确根据圆周角定理得到相等的角是关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
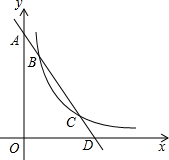 如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线
如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线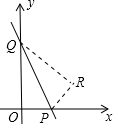 如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是
如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是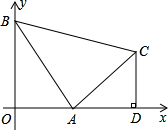 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F. 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.