题目内容
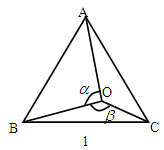
如图,点O是边长为1的等边△ABC内的任一点,设∠AOB= °,∠BOC=
°,∠BOC= °
°
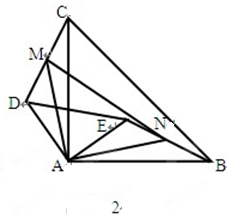
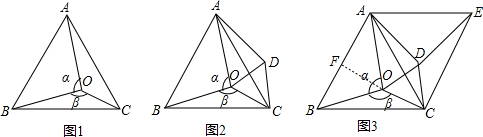
(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。
(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE
(3)在(2)的基础上, 当 、
、 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
 °,∠BOC=
°,∠BOC= °
°
(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。
(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE
(3)在(2)的基础上, 当
 、
、 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。(1)证明见解析;(2)证明见解析;(3)∠α=∠β=120°,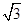 .
.
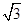 .
.试题分析:(1)根据旋转的性质就可以得出∠DOC=60°,OC=CD,进一步可以得出△DCO为等边三角形,即可以得出结论;
(2)根据旋转的性质就可以得出△ADC≌△BOC,△EAC≌△ABC,再由全等的性质可以得出△EAD≌△ABO,从而就可以得出结论;
(3)根据旋转的性质就可以得出△ADC≌△BOC,△EAD≌△ABO,就可以得出∠α=∠β=120°,再利用勾股定理就可以求出结论.
试题解析:(1)∵△BOC绕点C沿顺时针方向旋转60°得△ADC,
∴CO=CD,∠DOC=60°,
∴△COD是等边三角形,
∴DO=CO;
(2)∵△BOC绕点C沿顺时针方向旋转60°得△EDC,△ABC绕点C沿顺时针方向旋转60°得△EAC,
∴△ADC≌△BOC,△EAC≌△ABC,
∴AD=BO,∠DAC=∠OBC,EA=AB,∠EAC=∠ABC,
∴∠EAC-∠DAC=∠ABC-∠OBC,
即∠DAE=∠OBA,
在△EAD和△ABO中,
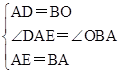 ,
,∴△EAD≌△ABO,
∴OA=DE;
(3)∵△ABC绕点C沿顺时针方向旋转60°得△EAC,
∴AB=BC=CE=AE,
∴四边形ABCE是菱形.
∵B、O、D、E在同一直线上,
∴B、O、D、E是菱形ABCE的对角线,
∴∠ABO=30°.
∵△ADC≌△BOC,△EAC≌△ABC,
∴∠ADC=∠BOC=β,∠ADE=∠AOB=α,
∴∠CDE=360°-α-β.
∵△COD是正三角形,
∴∠COD=∠CDO=60°.
∵点B、O、D、E在同一直线上,
∴∠BOC=∠CDE=120°,
∴∠ADC=120°,
∴∠ADE=120°,
∴α=β=120°.
∴∠BAO=30°.
∴∠BAO=∠ABO,
∴AO=BO,
同理可得:AO=CO.
∴AO=BO=CO.
作OF⊥AB于F,设BF=a,则BO=2a,
∴∠BFO=90°,BF=
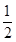 AB=
AB=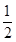
在Rt△BOF中,由勾股定理,得
a=
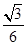 ,
,∴BO=
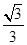 ,
,∴AO+BO+CO=
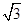 ,
,即AO+BO+CO的最小值为
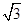 .
.
考点: 1.全等三角形的判定与性质;2.等边三角形的性质;3.旋转的性质.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目