题目内容
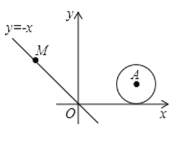
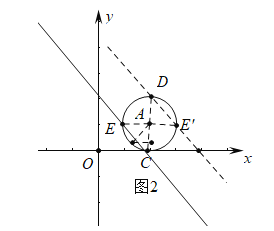
【题目】如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(2,1).直线OM是一次函数y=-x的图象.将直线OM沿x轴正方向平行移动.
(1)填空:直线OM与x轴所夹的锐角度数为 °;
(2)求出运动过程中⊙A与直线OM相切时的直线OM的函数关系式;(可直接用(1)中的结论)
(3)运动过程中,当⊙A与直线OM相交所得的弦对的圆心角为90°时,直线OM的函数关系式.
【答案】(1)45;(2) y=-x+3-![]() 或y=-x+3+
或y=-x+3+![]() ;(3) y=-x+2或y=-x+4.
;(3) y=-x+2或y=-x+4.
【解析】
(1)利用直线y=x上点的坐标特征易得直线y=x为第二、三四象限的角平分线,则直线OM与x轴所夹的锐角度数为45°;
(2)如图1中,设⊙A与x轴相切于点C,平移后的直线OM与⊙A相切于点E,交x轴于P,连接AE,AC,作ED⊥AC于D.求出点E坐标,利用待定系数法即可解决问题,再根据对称性解决另一种相切情形;
(3)当平移后的直线OM经过点C(⊙A与x轴的切点)时,弦EC所对的圆心角为90°,此时直线EC的解析式为y=x+2.再根据对称性解决另一种情形.
解:(1)∵直线y=-x上点到x轴和y轴的距离相等,
∴直线y=x为第二、四象限的角平分线,
∴直线OM与x轴所夹的锐角度数为45°;
故答案为45.
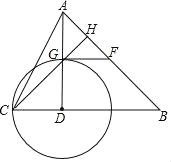
(2)如图1中,设⊙A与x轴相切于点C,平移后的直线OM与⊙A相切于点E,交x轴于P,连接AE,AC,作ED⊥AC于D.

∵∠OPE=45°,
∴∠EPC=135°,
∵∠AEP=∠ACP=90°,
∴∠EAD=45°,
∵AE=1,
∴AD=DE=![]()
∴CD=1-![]()
∴E(2-![]() ,1-
,1-![]() ),
),
设直线PE的解析式为y=-x+b,
则有1-![]() =-(2-
=-(2-![]() )+b,
)+b,
∴b=3-![]() ,
,
∴平移后直线OM的解析式为y=-x+3-![]() .
.
根据对称性可知,直线PE向右平移![]() 个单位直线与⊙A相切于点E′,此时直线OM的解析式为y=-x+3+
个单位直线与⊙A相切于点E′,此时直线OM的解析式为y=-x+3+![]() .
.
综上所述,运动过程中⊙A与直线OM相切时的直线OM的函数关系式为y=-x+3-![]() 或y=-x+3+
或y=-x+3+![]() .
.
(3)当平移后的直线OM经过点C(⊙A与x轴的切点)时,弦EC所对的圆角为90°,此时直线EC的解析式为y=-x+2.
根据对称性可知,当直线EC继续向右平移2个单位,与⊙A交于点D,E′,此时∠DAE′=90°,此时直线的解析式为y=-x+4.
综上所述,满足条件的直线OM的解析式为:y=-x+2或y=-x+4.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】《国家学生体质健康标准》规定:体质测试成绩达到90.0分及以上的为优秀;达到80.0分至89.9分的为良好;达到60.0分至79.9分的为及格;59.9分及以下为不及格,某校为了了解九年级学生体质健康状况,从该校九年级学生中随机抽取了10%的学生进行体质测试,测试结果如下面的统计表和扇形统计图所示。
各等级学生平均分统计表
等级 | 优秀 | 良好 | 及格 | 不及格 |
平均分 | 92.1 | 85.0 | 69.2 | 41.3 |
各等级学生人数分布扇形统计图

(1)扇形统计图中“不及格”所占的百分比是 ;
(2)计算所抽取的学生的测试成绩的平均分;
(3)若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数,请估计该九年级学生中约有多少人达到优秀等级。
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3