题目内容
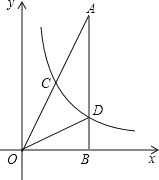
【题目】如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=![]() (k>0,x>0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是( )
(k>0,x>0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是( )
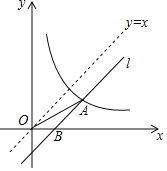
A.15B.5C.20D.10
【答案】D
【解析】
先利用函数图象“上加下减”的平移规律,得出直线l的方程为y=x﹣b,与反比例函数联立消去y后,得到关于x的方程,整理后得到x2=bx+k,并令直线l方程中y=0,求出x的值,确定出B的坐标,得出OB2,设出A的坐标,利用勾股定理表示出OA2,化简OA2﹣OB2=2k,由OA2﹣OB2=20,即可求出k的值.
解:直线y=x向下平移b个单位后得直线l:y=x﹣b,
∴B(b,0),
∵l与反比例函数y=![]() (k>0,x>0)的图象相交于点A,
(k>0,x>0)的图象相交于点A,
∴x﹣b=![]() ,则x2﹣bx﹣k=0.
,则x2﹣bx﹣k=0.
∴x2=bx+k.
设点A的坐标为(x,x﹣b),
∵OA2﹣OB2=x2+(x﹣b)2﹣b2=2x2﹣2bx=2(bx+k)﹣2bx=2k,OA2﹣OB2=20,
∴2k=20,
∴k=10.
故选:D.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?