题目内容
如图，点A、B、C在一次函数y=-4x+k的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是
- A.1
- B.6
- C.3（k+1）
- D.2（k-2）
B
分析：设AD⊥y轴于点D；BF⊥CF于点F，然后求出A、B、C、D、E、F、G各点的坐标，计算出长度，利用面积公式即可计算出．
解答：
解：由题意可得：A点坐标为（-1，4+k），B点坐标为（1，-4+k），C点坐标为（2，-8+k），D点坐标为（0，4+k），E点坐标为（0，k），F点坐标为（0，-4+k），G点坐标为（1，-4+k）．
所以，DE=EF=BG=4+k-k=k-（-4+k）=-4+k-（-8+k）=4，又因为AD=BE=GC=1，所以图中阴影部分的面积和等于
×4×1×3=6．
故选：B．
点评：本题主要考查了一次函数点的坐标的求法和三角形面积的求法．关键是掌握凡是函数图象上的点必能满足解析式．
分析：设AD⊥y轴于点D；BF⊥CF于点F，然后求出A、B、C、D、E、F、G各点的坐标，计算出长度，利用面积公式即可计算出．
解答：
解：由题意可得：A点坐标为（-1，4+k），B点坐标为（1，-4+k），C点坐标为（2，-8+k），D点坐标为（0，4+k），E点坐标为（0，k），F点坐标为（0，-4+k），G点坐标为（1，-4+k）．所以，DE=EF=BG=4+k-k=k-（-4+k）=-4+k-（-8+k）=4，又因为AD=BE=GC=1，所以图中阴影部分的面积和等于
×4×1×3=6．故选：B．
点评：本题主要考查了一次函数点的坐标的求法和三角形面积的求法．关键是掌握凡是函数图象上的点必能满足解析式．
练习册系列答案
阅读快车系列答案
相关题目
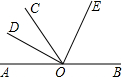如图，点A，O，B在同一直线上，射线OD平分∠AOC，射线OE平分∠BOC．
如图，点A、B、C在⊙O上，AO∥BC，∠OBC=40°，则∠ACB的度数是
（2012•北京）已知：如图，点E，A，C在同一直线上，AB∥CD，AB=CE，AC=CD．
（2012•鞍山）如图，点G、E、F分别在平行四边形ABCD的边AD、DC和BC上，DG=DC，CE=CF，点P是射线GC上一点，连接FP，EP．
（2013•南通二模）如图，点A是双曲线y=