��Ŀ����
��֪����ͼ��ֱ������ABCD�У�AD��BC����B=90�㣬AB=8��AD=12��tanC=| 4 | 3 |
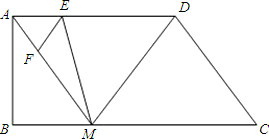 ��F�ֱ����߶�AD��AM�ϵĶ��㣨��E��A��D���غϣ��ҡ�FEM=��AMB����DE=x��MF=y��
��F�ֱ����߶�AD��AM�ϵĶ��㣨��E��A��D���غϣ��ҡ�FEM=��AMB����DE=x��MF=y����1����֤��AM=DM��
��2����y��x�ĺ�����ϵʽ��д��������
��3������E�ڱ�AD���ƶ�ʱ����EFMΪ���������Σ���x��ֵ��
��4������BMΪ�뾶�ġ�M����EDΪ�뾶�ġ�E���У����EMD�������
��������1������Ҫͨ������ȫ����������⣬��M��MG��AD��G����AG=BM����Rt��ABM�У��ɡ�AMB������C��������ֵ�����BM�ij���Ҳ�͵õ���AG�ij�����ʱ����G��AD���е㣬����֤�á�MAG�ա�MDG���ɴ˿ɵõ�����Ľ��ۣ�
��2������AD��BC���á�MAE=��FEM=��AMB������֤�á�AEM�ס�EFM���ֱ��ʾ��ME2��MF��MA�ij����������������εõ��ı����߶μ��ɵõ�y��x�ĺ�����ϵʽ��
��3�����������ε��������֪����EFM����FAE=��FEM�����EM��FM�����Է�����������ۼ��ɣ�
��EF=EM����ʱ��EFM=��EMF�����ڡ�EFM=��AEF=��FEM+��AEF���ɴ˿�֤��AE=MA=10���ɴ˿ɵõ�DE�ij���
��EF=FM����ʱ��FEM=��EMF=��EAM����AE=EM�����������߶εı���ʽ��ȣ�������ô�ʱDE�ij���
��4������Ҫ������������ۣ�
����Բ���У���ôEM=BM+DE���ֱ��ʾ�����߶εij�����������ĵ�����ϵ�з������x��ֵ�����ɵõ�DE�ij�����DEΪ�ס�ABΪ���ɵá�EMD�������
����Բ���У�����ͬ�ϣ�
��2������AD��BC���á�MAE=��FEM=��AMB������֤�á�AEM�ס�EFM���ֱ��ʾ��ME2��MF��MA�ij����������������εõ��ı����߶μ��ɵõ�y��x�ĺ�����ϵʽ��
��3�����������ε��������֪����EFM����FAE=��FEM�����EM��FM�����Է�����������ۼ��ɣ�
��EF=EM����ʱ��EFM=��EMF�����ڡ�EFM=��AEF=��FEM+��AEF���ɴ˿�֤��AE=MA=10���ɴ˿ɵõ�DE�ij���
��EF=FM����ʱ��FEM=��EMF=��EAM����AE=EM�����������߶εı���ʽ��ȣ�������ô�ʱDE�ij���
��4������Ҫ������������ۣ�
����Բ���У���ôEM=BM+DE���ֱ��ʾ�����߶εij�����������ĵ�����ϵ�з������x��ֵ�����ɵõ�DE�ij�����DEΪ�ס�ABΪ���ɵá�EMD�������
����Բ���У�����ͬ�ϣ�
����⣺��1��֤��������M��MG��AD��AD��G��
��AM��DC�����AMB=��C��
�ߡ�B=90�㣬AB=8��
��tan��AMB=tanC=
��
��
=
����BM=6����1�֣�
��AD��BC��AB��MG��
��AG=BM=6��
��AD=12����AG=GD����1�֣�
���AGM�ա�DGM��
��AM=DM����1�֣�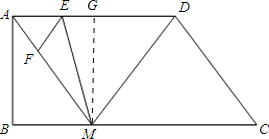
��2���ߡ�FEM=��AMB����AMB=��MAE��
���MAE=��MEF��
�ߡ�AME=��EMF��
���AEM�ס�EFM����1�֣�
��
=
��
��AM=
=10EM=
��
��
=
��
��y=
x2-
x+10����1�֣�
������Ϊ��0��x��12����1�֣�
��3���ߡ�EFM=��MAE+��AEF����FEM��
��EM��FM��
������EFMΪ���������Σ���EF=EM��EF=FM����1�֣�
�ٵ�EF=FMʱ��
12-x=10����x=2����2�֣�
�ڵ�EF=EMʱ��
�ߡ�FME=��FEM=��MAE��
��AE=EM��
��12-x=
��
��x=
����2�֣�
��4������M���E������x+6=
��
��x=
����1�֣�
��S��EMD=
����1�֣�
����M���E������(x-6)=
��
�����⣮��1�֣�
��AM��DC�����AMB=��C��
�ߡ�B=90�㣬AB=8��
��tan��AMB=tanC=
| AB |
| BM |
��
| 4 |
| 3 |
| 8 |
| BM |
��AD��BC��AB��MG��
��AG=BM=6��
��AD=12����AG=GD����1�֣�
���AGM�ա�DGM��
��AM=DM����1�֣�

��2���ߡ�FEM=��AMB����AMB=��MAE��
���MAE=��MEF��
�ߡ�AME=��EMF��
���AEM�ס�EFM����1�֣�
��
| AM |
| EM |
| EM |
| FM |
��AM=
| 62+82 |
| 82+(x-6)2 |
��
| 10 | ||
|
| ||
| y |
��y=
| 1 |
| 10 |
| 6 |
| 5 |
������Ϊ��0��x��12����1�֣�
��3���ߡ�EFM=��MAE+��AEF����FEM��
��EM��FM��
������EFMΪ���������Σ���EF=EM��EF=FM����1�֣�
�ٵ�EF=FMʱ��
12-x=10����x=2����2�֣�
�ڵ�EF=EMʱ��
�ߡ�FME=��FEM=��MAE��
��AE=EM��
��12-x=
| 82+(x-6)2 |
��x=
| 11 |
| 3 |
��4������M���E������x+6=
| 82+(x-6)2 |
��x=
| 8 |
| 3 |
��S��EMD=
| 32 |
| 3 |
����M���E������(x-6)=
| 82+(x-6)2 |
�����⣮��1�֣�
���������⿼����ȫ�������ε��ж������ʡ�ֱ�����ε����ʡ��Լ����������Ρ�ȫ�������ε��ж������ʣ�Բ��Բ��λ�ù�ϵ��֪ʶ���ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ
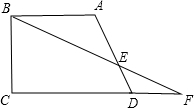 ��֪����ͼ��ֱ������ABCD�У���BCD=90�㣬��CDA=60�㣬AB=AD��AB=4��DF=2����BF�ij���
��֪����ͼ��ֱ������ABCD�У���BCD=90�㣬��CDA=60�㣬AB=AD��AB=4��DF=2����BF�ij���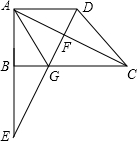
 ��֪����ͼ��ֱ������ABCD�У�AD��BC����ABC=90�㣬��ABΪֱ���ġ�O��DC����E�㣬AD=3cm��BC=5cm�����O�������
��֪����ͼ��ֱ������ABCD�У�AD��BC����ABC=90�㣬��ABΪֱ���ġ�O��DC����E�㣬AD=3cm��BC=5cm�����O�������