题目内容
已知正n边形的周长为60,边长为a。
(1)当n=3时,请直接写出a的值;
(2)若把正n边形的周长与边数同时增加7后,仍得到正多边形,它的边长记为b。问是否存在n使得a=b?若存在,求出n的值;若不存在,说明理由。
(1)当n=3时,请直接写出a的值;
(2)若把正n边形的周长与边数同时增加7后,仍得到正多边形,它的边长记为b。问是否存在n使得a=b?若存在,求出n的值;若不存在,说明理由。
解:(1)a=20;
(2)存在,
当a=b,得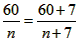
即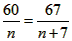 ,
,
∴ 60n+420=67n,解得n=60,
经检验n=60是方程的根,
∴ 当n=60时,a=b,即不符合这一说法的n的值为60。
(2)存在,
当a=b,得
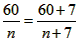
即
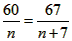 ,
,∴ 60n+420=67n,解得n=60,
经检验n=60是方程的根,
∴ 当n=60时,a=b,即不符合这一说法的n的值为60。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目