题目内容
已知正n边形的周长为60，边长为a
（1）当n=3时，请直接写出a的值；
（2）把正n边形的周长与边数同时增加7后，假设得到的仍是正多边形，它的边数为n+7，周长为67，边长为b．有人分别取n等于3，20，120，再求出相应的a与b，然后断言：“无论n取任何大于2的正整数，a与b一定不相等．”你认为这种说法对吗？若不对，请求出不符合这一说法的n的值．
解：（1）a=20；
（2）此说法不正确．
理由如下：尽管当n=3，20，120时，a＞b或a＜b，
但可令a=b，得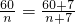
，即
．
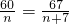∴60n+420=67n，解得n=60，
经检验n=60是方程的根．
∴当n=60时，a=b，即不符合这一说法的n的值为60．
分析：（1）边长=周长÷边数；
（2）分别表示出a和b的代数式，让其相等，看是否有相应的值．
点评：读懂题意，找到相应量的等量关系是解决问题的关键．
（2）此说法不正确．
理由如下：尽管当n=3，20，120时，a＞b或a＜b，
但可令a=b，得
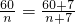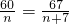，即．∴60n+420=67n，解得n=60，
经检验n=60是方程的根．
∴当n=60时，a=b，即不符合这一说法的n的值为60．
分析：（1）边长=周长÷边数；
（2）分别表示出a和b的代数式，让其相等，看是否有相应的值．
点评：读懂题意，找到相应量的等量关系是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目