题目内容
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.

(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
【答案】(1)108°,72°,108°,72°. (2)图形见解析(3)∠BAD的度数为80°.
【解析】试题分析:(1)先由对角线AC是黄金线,可知△ABC是等腰三角形,分两种情况讨论:①AB=BC;②AC=BC.根据黄金四边形的定义和四边形的内角和求解即可;
(2)①以A为圆心,AC为半径画弧,交圆O于D1,②以C为圆心,AC为半径画弧,交圆O于D2,③连接AD1,CD1,AD2,CD2.
(3)先根据∠BAC=30°,算得∠ABC=120°,再分情况讨论:
i:当AC为黄金线,则AD=CD,或AD=AC,根据等腰三角形及黄金四边形进行计算即可;ii:当BD为黄金线时,分三种情况:①当AB=AD时,②当AB=BD时,③当AD=dD时。
试题解析:(1)∵在四边形ABCD中,对角线AC是黄金线,
∴△ABC是等腰三角形,
∵AB<AC,
∴AB=BC或AC=BC,
①当AB=BC时,
∵AB=AD=DC,
∴AB=BC=AD=DC,
又∵AC=AC,
∴△ABC≌△ADC,
此种情况不符合黄金四边形定义,
②AC=BC,
同理,BD=BC,
∴AC=BD=BC,易证得△ABD≌△DAC,△CAB≌△BDC,
∴∠DAC=∠DCA=∠ABD=∠ADB,∠BDC=∠BCD=∠CAB=∠CBA,
且∠DCA<∠DCB,
∴∠DAC<∠CAB
又由黄金四边形定义知:∠CAB=2∠DAC,
设∠DAC=∠DCA=∠ABD=∠ADB=x°,
则∠BDC=∠BCD=∠CAB=∠CBA=2x°,
∴∠DAB=∠ADC=3x°,
而四边形的内角和为360°,
∴∠DAB=∠ADC=108°,∠BCD=∠CBA=72°,
答:四边形ABCD各个内角的度数分别为108°,72°,108°,72°.
(2)由题意作图为: 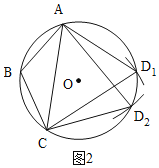
(3)∵AB=BC,∠BAC=30°,
∴∠BCA=∠BAC=30°,∠ABC=120°,
ⅰ)当AC为黄金线时,
∴△ACD是等腰三角形,
∵AB=BC=CD,AC>BC,
∴AD=CD或AD=AC,
当AD=CD时,则AB=BC=CD=AD,
又∵AC=AC,
∴△ABC≌△ADC,
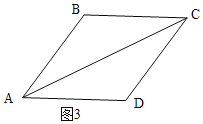
如图3,此种情况不符合黄金四边形定义,
∴AD≠CD,
当AD=AC时,由黄金四边形定义知,∠ACD=∠D=15°或60°,
此时∠BAD=180°(不合题意,舍去)或90°(不合题意,舍去);
ⅱ)当BD为黄金线时,
∴△ABD是等腰三角形,
∵AB=BC=CD,
∴∠CBD=∠CDB,
①当AB=AD时,△BCD≌△BAD,
此种情况不符合黄金四边形定义;
②当AB=BD时,AB=BD=BC=CD,
∴△BCD是等边三角形,
∴∠CBD=60°,
∴∠A=30°或120°(不合题意,舍去),
∴∠ABC=180°(不合题意,舍去),
此种情况也不符合黄金四边形定义;
③当AD=BD时,设∠CBD=∠CDB=y°,则∠ABD=∠BAD=(2y)°或![]() ,
,
∵∠ABC=∠CBD+∠ABD=120°,
当∠ABD=2y°时,y=40,
∴∠BAD=2y=80°;
当![]() 时,y=80°,
时,y=80°,
∴![]() ;
;
由于∠ADB=180°-40°-40°=100°,
∠BDC=80°,
∴∠ADB+∠BDC=180°,
∴此种情况不能构成四边形,
综上所述:∠BAD的度数为80°.

 阅读快车系列答案
阅读快车系列答案


