题目内容
如图,已知O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB平分线,求∠DOE的度数.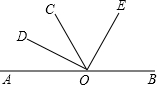
分析:根据图示确立各角度数之间的关系,然后求出∠DOE的度数.
解答:解:O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB平分线,
∴∠AOB=180°∠DOC=
∠AOC∠EOC=
∠BOC,
∠DOE=∠DOC+∠EOC=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB=90°.
故答案为90°.
∴∠AOB=180°∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
∠DOE=∠DOC+∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为90°.
点评:根据图示确立各角度数之间的关系,利用角平分线的性质来求.

练习册系列答案
相关题目
 2、如图,已知O是直线CD上的点,OA平分∠BOC,∠AOC=35°,则∠BOD的度数.
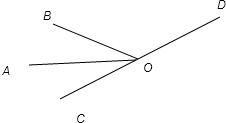
2、如图,已知O是直线CD上的点,OA平分∠BOC,∠AOC=35°,则∠BOD的度数.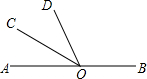 如图,已知O是直线AB上一点,∠COD=35°,且∠COD:∠BOD=1:3,则∠AOC的度数为( )
如图,已知O是直线AB上一点,∠COD=35°,且∠COD:∠BOD=1:3,则∠AOC的度数为( ) 如图,已知A是直线l外的一点,B是l上的一点.
如图,已知A是直线l外的一点,B是l上的一点.