Question

【题目】如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于82°，则∠OBC=°．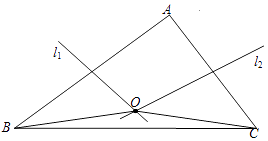

Answer 1

【答案】8
【解析】解：连接OA，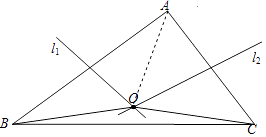
∵∠BAC=82°，
∴∠ABC+∠ACB=180°﹣82°=98°，
∵AB、AC的垂直平分线交于点O，
∴OB=OA，OC=OA，
∴∠OAB=∠OBA，∠OAC=∠OCA，
∴∠OBC+∠OCB=100°﹣（OBA+∠OCA）=16°，
∴∠OBC=8°，
所以答案是：8．
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题．