题目内容
分式化简:
(1)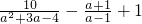
(2) (a-b+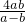 )(a+b-
)(a+b-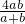 )
)
(3)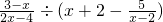
(4)先化简,再求值: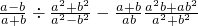 ,其中a,b满足a2+b2+a-4b+
,其中a,b满足a2+b2+a-4b+ =0.
=0.
解:(1)原式=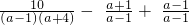
=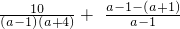
=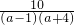 -
-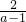
=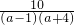 -
-
=
=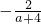 ;
;
(2)原式=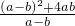 •
•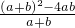 =
=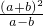 •
•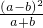 =(a+b)(a-b)=a2-b2;
=(a+b)(a-b)=a2-b2;
(3)原式=
=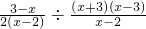
=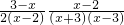
=-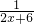 ;
;
(4)原式=
=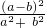 -
-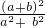
=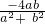
又a2+b2+a-4b+ =0,故(a2+a+
=0,故(a2+a+ )+(b2-4b+4)=0即
)+(b2-4b+4)=0即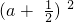 +(b-2)2=0
+(b-2)2=0
可得a= b=2
b=2
此时原式= =
=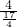 =
=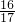 .
.
分析:(1)找到最简公分母进行通分,然后加减运算,
(2)把括号因式进行通分,然后进行乘法运算,进行约分化简,
(3)首先把括号里因式进行通分,然后把除法运算转化成乘法运算,进行约分化简.
(4)首先进行乘除运算,能分解因式的因子先分解因式,进行约分,然后进行减法运算,最后代值计算.
点评:这类题主要考查分式的化简求值,做这些混合运算时一定要注意运算顺序.最后一题的配方法应熟练应用,总之这是一类十分好的题,一定要注意练习.
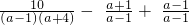
=
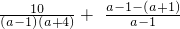
=
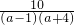 -
-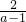
=
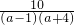 -
-
=

=
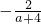 ;
;(2)原式=
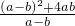 •
•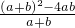 =
=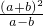 •
•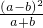 =(a+b)(a-b)=a2-b2;
=(a+b)(a-b)=a2-b2;(3)原式=

=
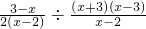
=
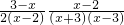
=-
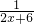 ;
;(4)原式=

=
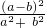 -
-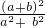
=
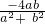
又a2+b2+a-4b+
 =0,故(a2+a+
=0,故(a2+a+ )+(b2-4b+4)=0即
)+(b2-4b+4)=0即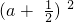 +(b-2)2=0
+(b-2)2=0可得a=
 b=2
b=2此时原式=
 =
=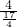 =
=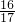 .
.分析:(1)找到最简公分母进行通分,然后加减运算,
(2)把括号因式进行通分,然后进行乘法运算,进行约分化简,
(3)首先把括号里因式进行通分,然后把除法运算转化成乘法运算,进行约分化简.
(4)首先进行乘除运算,能分解因式的因子先分解因式,进行约分,然后进行减法运算,最后代值计算.
点评:这类题主要考查分式的化简求值,做这些混合运算时一定要注意运算顺序.最后一题的配方法应熟练应用,总之这是一类十分好的题,一定要注意练习.

练习册系列答案
相关题目